 Problem K. 268. (November 2010)
Problem K. 268. (November 2010)
K. 268. How long is the radius of the circle in which a chord of length 6 units is twice as far away from the centre as a chord of length 12 units?
(6 pont)
Deadline expired on December 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
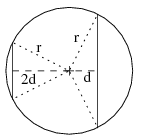
Megoldás. A húrok szimmetriatengelye és a végpontokba a kör középpontjából húzott szakaszok derékszögű háromszögeket határoznak meg (ld. ábra), melyekben Pithagorasz tételét felírva: \(\displaystyle 4d^2 + 9 =r^2 = d^2 +36\), ahonnan \(\displaystyle d^2=9\), azaz (\(\displaystyle d>0\) miatt) \(\displaystyle d=3\). Ezért a kör sugara \(\displaystyle \sqrt 5\), a két húr távolsága pedig \(\displaystyle 3\sqrt 5\).
Statistics:
204 students sent a solution. 6 points: 77 students. 5 points: 45 students. 4 points: 13 students. 3 points: 32 students. 2 points: 15 students. 1 point: 1 student. 0 point: 12 students. Unfair, not evaluated: 9 solutionss.
Problems in Mathematics of KöMaL, November 2010
