Problem K. 557. (October 2017)

K. 557. The midpoints of the sides of a square \(\displaystyle ABCD\) are \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) and \(\displaystyle S\). They are connected to the vertices of the square as shown in the figure. Prove that \(\displaystyle AT = TV\).

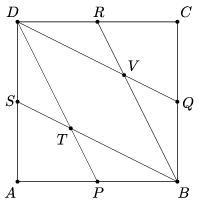
(6 pont)

Deadline expired on November 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

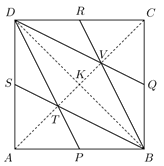
Megoldás. Szimmetria miatt \(\displaystyle T\) és \(\displaystyle V\) az \(\displaystyle AC\) átló egyenesén vannak, \(\displaystyle AK=KC\) és \(\displaystyle TK=KV\).

Az \(\displaystyle ABD\) háromszögnek \(\displaystyle T\) a súlypontja, mert \(\displaystyle BS\) és \(\displaystyle DP\) súlyvonalak. A \(\displaystyle DBC\) háromszögnek \(\displaystyle V\) a súlypontja, mert \(\displaystyle BR\) és \(\displaystyle DQ\) súlyvonalak. A háromszög súlypontja a csúcstól távolabbi harmadoló pont a súlyvonalon. Ezért \(\displaystyle AT = 2TK=TK+ KV =TV\).

Statistics:

122 students sent a solution.
6 points:	53 students.
5 points:	22 students.
4 points:	13 students.
3 points:	7 students.
2 points:	6 students.
1 point:	8 students.
0 point:	1 student.
Unfair, not evaluated:	12 solutionss.

Problems in Mathematics of KöMaL, October 2017