 |
A K. 566. feladat (2017. december) |
K. 566. Az \(\displaystyle ABCD\) négyszög oldalai \(\displaystyle AB = 8\) cm, \(\displaystyle BC= 7\) cm, \(\displaystyle CD = 6\) cm és \(\displaystyle DA = 5\) cm hosszúak. Az \(\displaystyle BCD\) és \(\displaystyle ABD\) háromszögek beírható köre a \(\displaystyle BD\) átlót rendre az \(\displaystyle E\) és \(\displaystyle F\) pontokban érinti. Milyen hosszú az \(\displaystyle EF\) szakasz?
(6 pont)
A beküldési határidő 2018. január 10-én LEJÁRT.
Megoldás. Egy körhöz egy külső pontból húzott érintőszakaszok hossza egyenlő.
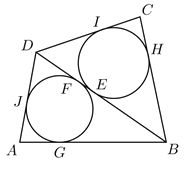
Az \(\displaystyle ABD\) háromszögben \(\displaystyle AG = AJ\), \(\displaystyle GB = BF = 8 – AG\), valamint \(\displaystyle JD = DF = 5-AJ=5 – AG\), így \(\displaystyle DB = (5– AG) + (8 – AG) = 13 – 2AG\).
A \(\displaystyle BCD\) háromszögben hasonlóan \(\displaystyle DB = (7– CH) + (6 – CH) = 13 – 2CH\), így \(\displaystyle AG = CH\).
\(\displaystyle FE = DB – DF – BE = 13 – 2AG – (5 – AG) – (7 – CH) = 1\).
Statisztika:
75 dolgozat érkezett. 6 pontot kapott: 62 versenyző. 5 pontot kapott: 2 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 6 versenyző.
A KöMaL 2017. decemberi matematika feladatai

