Problem K. 566. (December 2017)

K. 566. The lengths of the sides of a quadrilateral \(\displaystyle ABCD\) are \(\displaystyle AB = 8\) cm, \(\displaystyle BC= 7\) cm, \(\displaystyle CD = 6\) cm and \(\displaystyle DA = 5\) cm. The inscribed circles of triangles \(\displaystyle BCD\) and \(\displaystyle ABD\) touch diagonal \(\displaystyle BD\) at points \(\displaystyle E\) and \(\displaystyle F\), respectively. What is the length of the line segment \(\displaystyle EF\)?

(6 pont)

Deadline expired on January 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Egy körhöz egy külső pontból húzott érintőszakaszok hossza egyenlő.

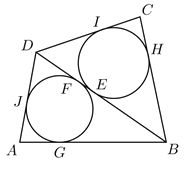
Az \(\displaystyle ABD\) háromszögben \(\displaystyle AG = AJ\), \(\displaystyle GB = BF = 8 – AG\), valamint \(\displaystyle JD = DF = 5-AJ=5 – AG\), így \(\displaystyle DB = (5– AG) + (8 – AG) = 13 – 2AG\).

A \(\displaystyle BCD\) háromszögben hasonlóan \(\displaystyle DB = (7– CH) + (6 – CH) = 13 – 2CH\), így \(\displaystyle AG = CH\).

\(\displaystyle FE = DB – DF – BE = 13 – 2AG – (5 – AG) – (7 – CH) = 1\).

Statistics:

75 students sent a solution.
6 points:	62 students.
5 points:	2 students.
2 points:	4 students.
1 point:	1 student.
0 point:	6 students.

Problems in Mathematics of KöMaL, December 2017