Problem K. 597. (October 2018)

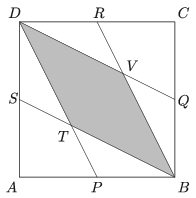
K. 597. The midpoints \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) and \(\displaystyle S\) of the sides of a square \(\displaystyle ABCD\) are connected to the vertices as shown in the figure. Determine the ratio of the area of quadrilateral \(\displaystyle BVDT\) to that of the square \(\displaystyle ABCD\).

(6 pont)

Deadline expired on November 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A \(\displaystyle DBC\triangle\)-nek \(\displaystyle V\) a súlypontja, így a \(\displaystyle DBV\triangle\) területe a \(\displaystyle DBC\triangle\) területének a harmada, hiszen a \(\displaystyle BD\) oldaluk közös és a \(\displaystyle V\) pont (a csúcstól távolabbi harmadoló pont a súlyvonalon, így a) távolsága \(\displaystyle DB\)-től harmadannyi, mint a \(\displaystyle C\) pont távolsága, vagyis a \(\displaystyle DBV\triangle\) \(\displaystyle DB\) oldalhoz tartozó magassága harmada a \(\displaystyle DBC\) háromszög \(\displaystyle DB\) oldalhoz tartozó magasságának. Hasonló igaz a \(\displaystyle DBT\triangle\) területére, így a \(\displaystyle BVDT\) négyszög területe harmada az \(\displaystyle ABCD\) négyzet területének.

Statistics:

169 students sent a solution.
6 points:	51 students.
5 points:	14 students.
4 points:	14 students.
3 points:	21 students.
2 points:	15 students.
1 point:	13 students.
0 point:	14 students.
Unfair, not evaluated:	5 solutionss.
Not shown because of missing birth date or parental permission:	22 solutions.

Problems in Mathematics of KöMaL, October 2018