 Problem K. 598. (October 2018)
Problem K. 598. (October 2018)
K. 598. On a digital clock display, digits consist of small illuminated line segments as shown in the figure.
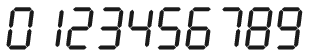
The energy consumption of the clock depends on the number of small line segments switched on or off as time elapses. For example, when a 3 changes to a 4, two line segments are switched off and one is switched on, which means 3 switch operations. During a full cycle of \(\displaystyle 0, 1, 2, \ldots, 9, 0\), this adds up to a total of 30 switch operations. If the same digit symbols were used to designate the numbers 0 to 9 in some different order, the number of switch operations could be reduced. Find the minimum number of switch operations that could be achieved in a full cycle, and give an example for a possible order of digits.
Proposed by Zs. Ruttkai, the Netherlands
(6 pont)
Deadline expired on November 12, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Két szám távolságán most a köztük lévő szükséges kapcsolások számát értjük. Minden számhoz megkeressük a hozzá legkisebb (1 vagy 2) távolságra lévő számokat. A táblázat első sorában és oszlopában a számok, a többi helyen ezek távolsága van (csak az 1 és 2 távolságok).
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 2 | 1 | 2 | |||||||
| 1 | 2 | 1 | ||||||||
| 2 | 2 | 2 | ||||||||
| 3 | 2 | 2 | 2 | 2 | 1 | |||||
| 4 | 2 | 2 | ||||||||
| 5 | 2 | 1 | 1 | |||||||
| 6 | 2 | 1 | 1 | 2 | ||||||
| 7 | 1 | 2 | ||||||||
| 8 | 1 | 2 | 2 | 1 | 1 | |||||
| 9 | 2 | 1 | 2 | 1 | 2 | 1 |
Mivel teljes ciklust kell leírnunk, minden szám előtt és után is kell állnia számnak (az elején és a végén ugyanaz a szám áll). Minden számhoz tartozik két legkisebb távolság, a sorában szereplő két legkisebb szám, ez a 0-nál 1 és 2, az 1-nél szintén 1 és 2, a 2-nél 2 és 2 stb. Ha ezeket összeadjuk, megkapjuk, hogy az adott szám minimum hány kapcsolással kivitelezhető a ciklusban. Ezek összege \(\displaystyle 3+3+4+3+4+2+2+3+2+2=28\). Ezt elosztva kettővel (mert minden távolságot kétszer számoltunk) megkapjuk azt az elméleti minimumot, aminél kevesebb kapcsolással biztosan nem vihető végbe a teljes ciklus. Ez az összeg \(\displaystyle \frac{28}{2}=14\). Azonban a megvalósítható minimum ennél nagyobb, a következők miatt. A 2-es előtt és után a fenti legkisebb távolságok miatt a 8-as és a 3-as áll (a sorrend mindegy), de a 8-asnál keletkező legkisebb távolságok összege, a 2 egység úgy jönne ki, ha a 8-as szomszédai a 6, a 9 vagy a 0 lennének, mert ezek vannak 1 távolságra tőle. Emiatt a 8-asnál számolt legkisebb távolságok összege 1-gyel nő. Hasonló okok miatt a 4-es előtt vagy után 9-esnek kell állnia, aminek a 2 egységnyi eredeti minimumát ez szintén növeli 1-gyel. A 9-es másik oldalán az elméleti minimum szerint a 3-nak és az 5-nek egyszerre kellene lennie, ez nem lehet, ezért vagy a hármasnál vagy az ötösnél ez újabb emelést jelent 1-gyel. Hasonló okok miatt a 8-as egyik oldalán mindenképp a 2-esnek kell állnia, ami miatt a másik oldalon az elméleti minimum szerint a 0-nak és a 6-nak egyszerre kellene lennie. Ez szintén növeli 1-gyel az elméleti minimumot. Az előbbiek alól kivételt csak az az eset képezne, ha a 2-esnél a 8 helyett egy másik szomszédot választanánk, de akkor ez már önmagában legalább 2-vel növeli a vizsgált összeget, hasonlóan a 4-esnek választhatunk a 9-es helyett másik szomszédot, de ez is tovább növelné a kapcsolások számát. Így az elméleti 28-as minimum (a 2-vel való osztás előtt) összesen legalább 4-gyel nőtt, azaz a valódi minimum \(\displaystyle \frac{32}{2}=16\).
Több olyan ciklus is elképzelhető, aminek a kapcsolási összege 16, egy példa: 14956082371.
Hoffmann Szabolcs (Egri Szilágyi E. Gimn., 9. évf.)
Statistics:
170 students sent a solution. 6 points: Egyházi Hanna, Hoffmann Szabolcs, Kalocsai Zoltán, Miklóssy Katinka, Toronyi András. 5 points: Ferjancsik Zaránd, Sebestyén Pál Botond, Szirmai Dénes. 4 points: 1 student. 3 points: 11 students. 2 points: 8 students. 1 point: 27 students. 0 point: 96 students. Not shown because of missing birth date or parental permission: 19 solutions.
Problems in Mathematics of KöMaL, October 2018
