 |
A K. 601. feladat (2018. november) |
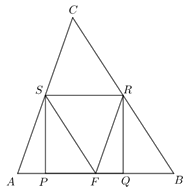
K. 601. Egy hegyesszögű \(\displaystyle ABC\) háromszögbe olyan 4 cm oldalhosszúságú \(\displaystyle PQRS\) négyzetet lehet írni, melynek \(\displaystyle P\) és \(\displaystyle Q\) csúcsa az \(\displaystyle AB\) oldalon, \(\displaystyle R\) csúcsa a \(\displaystyle BC\) oldalon, \(\displaystyle S\) csúcsa pedig az \(\displaystyle AC\) oldalon van. Mekkora a háromszög területe, ha az \(\displaystyle AB\) oldal hossza 8 cm?
(6 pont)
A beküldési határidő 2018. december 10-én LEJÁRT.
Megoldás. Jelölje \(\displaystyle F\) az \(\displaystyle AB\) oldal felezőpontját. \(\displaystyle AFBS\) és \(\displaystyle FBRS\) paralelogramma, hiszen két-két oldaluk 4 cm hosszú és párhuzamosak. Így \(\displaystyle SFRC\) is paralelogramma, hiszen szemközti oldalai párhuzamosak. Ezért az \(\displaystyle SRC\) háromszög egybevágó az \(\displaystyle RSF\) háromszöggel (az oldalaik páronként egyenlőek), így a területük egyenlő.
Hasonlóképpen az \(\displaystyle AFS\) és az \(\displaystyle SFR\), illetve az \(\displaystyle FBR\) és az \(\displaystyle RFS\) háromszögek is egybevágóak (az oldalaik páronként egyenlőek). Így az \(\displaystyle ABC\) háromszög területe az \(\displaystyle FBS\) háromszög területének a négyszerese, azaz \(\displaystyle 4\cdot(4\cdot 4:2)=32~\mathrm{cm}^2\).
Statisztika:
146 dolgozat érkezett. 6 pontot kapott: 86 versenyző. 5 pontot kapott: 12 versenyző. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 7 versenyző. Nem versenyszerű: 1 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 16 dolgozat.
A KöMaL 2018. novemberi matematika feladatai

