Problem K. 601. (November 2018)

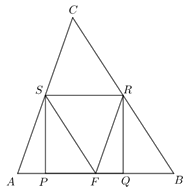
K. 601. The sides of a square \(\displaystyle PQRS\) inscribed in an acute-angled triangle \(\displaystyle ABC\) are 4 cm long, vertices \(\displaystyle P\) and \(\displaystyle Q\) lie on side \(\displaystyle AB\), vertex \(\displaystyle R\) lies on side \(\displaystyle BC\), and vertex \(\displaystyle S\) lies on side \(\displaystyle AC\). Given that the length of side \(\displaystyle AB\) is 8 cm, what is the area of the triangle?

(6 pont)

Deadline expired on December 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje \(\displaystyle F\) az \(\displaystyle AB\) oldal felezőpontját. \(\displaystyle AFBS\) és \(\displaystyle FBRS\) paralelogramma, hiszen két-két oldaluk 4 cm hosszú és párhuzamosak. Így \(\displaystyle SFRC\) is paralelogramma, hiszen szemközti oldalai párhuzamosak. Ezért az \(\displaystyle SRC\) háromszög egybevágó az \(\displaystyle RSF\) háromszöggel (az oldalaik páronként egyenlőek), így a területük egyenlő.

Hasonlóképpen az \(\displaystyle AFS\) és az \(\displaystyle SFR\), illetve az \(\displaystyle FBR\) és az \(\displaystyle RFS\) háromszögek is egybevágóak (az oldalaik páronként egyenlőek). Így az \(\displaystyle ABC\) háromszög területe az \(\displaystyle FBS\) háromszög területének a négyszerese, azaz \(\displaystyle 4\cdot(4\cdot 4:2)=32~\mathrm{cm}^2\).

Statistics:

146 students sent a solution.
6 points:	86 students.
5 points:	12 students.
4 points:	9 students.
3 points:	10 students.
2 points:	2 students.
1 point:	3 students.
0 point:	7 students.
Unfair, not evaluated:	1 solutions.
Not shown because of missing birth date or parental permission:	16 solutions.

Problems in Mathematics of KöMaL, November 2018