 |
A K. 606. feladat (2018. december) |
K. 606. Egy \(\displaystyle ABCDE\) ötszög \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\) és \(\displaystyle DE\) oldala egységnyi hosszúságú, az \(\displaystyle ABC\sphericalangle\) és a \(\displaystyle CDE\sphericalangle\) is \(\displaystyle 90^{\circ}\)-os. Mutassuk meg, hogy ilyen ötszögekkel hézagmentesen parkettázható a sík. Mutassuk meg konvex és konkáv esetre is.
(6 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
Megoldás. Az ötszög mindenképpen szimmetrikus, mert lényegében két derékszögű egyenlőszárú háromszög (az \(\displaystyle ABC\) és a \(\displaystyle CDE\)) hegyesszögű csúcsában való összeillesztéséből keletkezik.
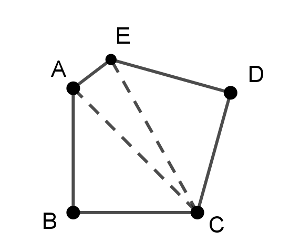
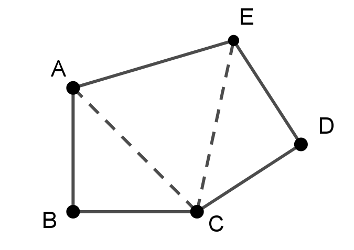
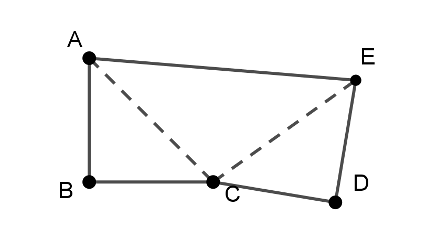
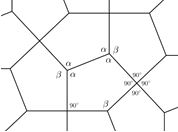
Az ötszög belső szögeinek összege \(\displaystyle 540^{\circ}\). A nem \(\displaystyle 90^{\circ}\)-os szögeinek összege \(\displaystyle 360^{\circ}\), így a csatlakozásuk az ábrán látható elrendezésben hézagmentes. Ugyanez igaz konkáv ötszög esetén is.
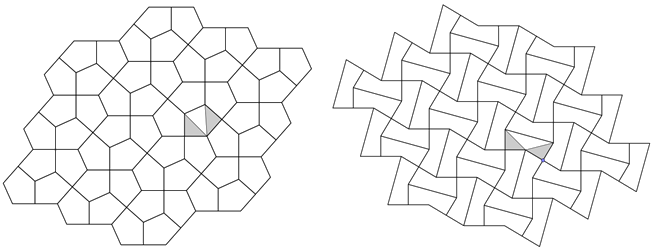

Statisztika:
75 dolgozat érkezett. 6 pontot kapott: Egyházi Hanna, Hoffmann Szabolcs, Kalocsai Zoltán, Kovács Brúnó Aurél, Lévay Anna, Ludvig Emese Ágota, Márky Anna, Mátéfy Ádám , Mohay Lili Veronika, Németh Máté Előd, Osváth Klára, Riba Dániel, Somogyi Dalma, Szabó 34 Péter Bence, Szirmai Dénes, Tarján Teréz, Varga 601 Zalán. 5 pontot kapott: Bodor 001 Bence Ádám, Cserkuti Sándor, Diczházi Noémi, Dózsa Levente, Gál Máté, Károly Kinga, Németh László Csaba, Rács Zsóka, Salamon Tamás Koppány, Sámuel Laura , Szabó Panna, Valkai Máté. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 21 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 5 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 7 dolgozat.
A KöMaL 2018. decemberi matematika feladatai

