A K. 617. feladat (2019. február)

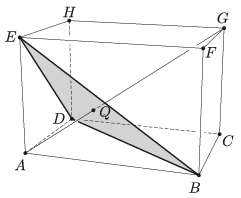
K. 617. Egy \(\displaystyle ABCDEFGH\) téglatest \(\displaystyle AG\) testátlója a \(\displaystyle BDE\) háromszöget a \(\displaystyle Q\) pontban metszi. Igazoljuk, hogy \(\displaystyle Q\) a \(\displaystyle BDE\) háromszög súlypontja.

(6 pont)

A beküldési határidő 2019. március 11-én LEJÁRT.

Megoldás. Az \(\displaystyle ACGE\) sík a \(\displaystyle BDE\) síkot annak \(\displaystyle EL\) egyenesében metszi, ahol \(\displaystyle L\) az egy síkban fekvő \(\displaystyle AC\) és \(\displaystyle BD\) egyenesek metszéspontja. Így \(\displaystyle AG\) és a \(\displaystyle BDE\) sík \(\displaystyle Q\) metszéspontja rajta kell, hogy legyen \(\displaystyle EL\)-en, ami a \(\displaystyle BDE\) háromszög egyik súlyvonala. Hasonlóan belátható, hogy a \(\displaystyle BDE\) háromszög többi súlyvonalán is rajta van \(\displaystyle Q\), így a \(\displaystyle Q\) pont valóban a \(\displaystyle BDE\) háromszög súlypontja.

Statisztika:

50 dolgozat érkezett.
6 pontot kapott:	Barát Benedek, Barczikay Ákos, Cserkuti Sándor, Dózsa Levente, Egyházi Hanna, Ferencz Lilla, Flódung Áron , Gál Máté, Hamar János, Hamvas Johanna Kata, Hegedűs András , Hoffmann Szabolcs, Kalocsai Zoltán, Leopold Rozvita, Malatinszki Hanna, Márky Anna, Metzger Ábris András, Mócsy Mátyás, Mohay Lili Veronika, Nagy Bianka , Németh László Csaba, Németh Máté Előd, Osváth Klára, Plósz István Marcell, Rács Zsóka, Riba Dániel, Salamon Tamás Koppány, Sárvári Borka Luca, Sebestyén Pál Botond, Somogyi Dalma, Szabó 003 Szabina, Szépvölgyi Gergely, Szirmai Dénes, Tarján Teréz, Xu Yiling.
4 pontot kapott:	4 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2019. februári matematika feladatai