Problem K. 623. (March 2019)

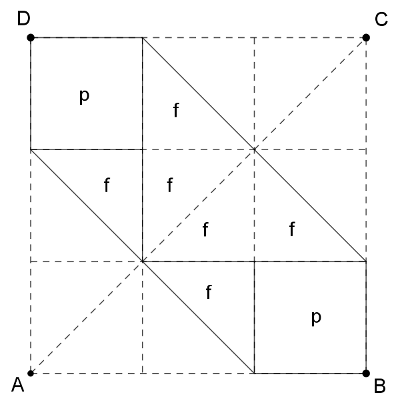
K. 623. The front side of a square sheet of paper \(\displaystyle ABCD\) is red, and the back side is white. \(\displaystyle E\) and \(\displaystyle F\) divide diagonal \(\displaystyle AC\) into three equal parts, with \(\displaystyle E\) lying closer to \(\displaystyle A\). The sheet is folded along lines perpendicular to \(\displaystyle AC\) by folding the back side towards the front (that is, making the back of the sheet appear on top). During the first folding, point \(\displaystyle A\) is moved to cover \(\displaystyle F\), and during the second folding, point \(\displaystyle C\) is moved to cover \(\displaystyle E\). What will be the ratio of the red area to the white area on the front side of the sheet in the end?

(6 pont)

Deadline expired on April 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A hajtások során piros marad a \(\displaystyle B\) és \(\displaystyle D\) csúcsoknál egy-egy \(\displaystyle 1/3\) négyzetoldalnyi piros négyzet, melyek területe összesen \(\displaystyle 2/9\) négyzetterületnyi. A hajtások során kapott papír látható területe a négyzet területének \(\displaystyle 5/9\) része (összesen egy \(\displaystyle 2/3\) négyzetoldalnyi négyzetet hajtottunk át). A piros és a teljes aránya \(\displaystyle \frac29:\frac59=\frac25\), tehát a piros és fehér rész aránya \(\displaystyle 2:3\).

Statistics:

116 students sent a solution.
6 points:	73 students.
5 points:	11 students.
4 points:	10 students.
3 points:	3 students.
1 point:	2 students.
0 point:	4 students.
Not shown because of missing birth date or parental permission:	13 solutions.

Problems in Mathematics of KöMaL, March 2019