 |
A K. 628. feladat (2019. szeptember) |
K. 628. Zoli négy egyforma téglalap alakú papírdarabból egy nagyobb téglalapot állított össze, a papírokat átfedés nélkül, hézagmentesen az asztalra helyezve. A kapott téglalap területe \(\displaystyle 1200~\mathrm{cm}^{2}\). Tudjuk, hogy a papírokat úgy helyezte el, hogy nem vihető át bármelyik papírdarab bármelyik papírdarabra csak eltolás segítségével. Mekkora a nagy téglalap kerülete?
(6 pont)
A beküldési határidő 2019. október 10-én LEJÁRT.
Megoldás. A négy téglalap a feltételeknek megfelelően lényegében háromféleképpen adhat ki egy nagyobbat, de a harmadik elrendezést az utolsó feltétel nem engedi meg.
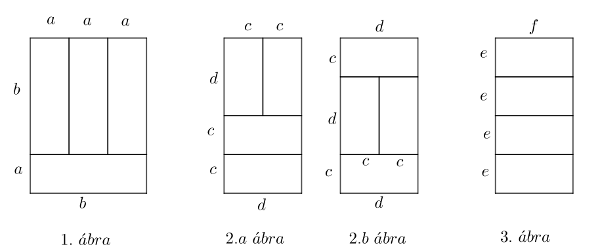
Az első elrendezés esetén \(\displaystyle b = 3a\), \(\displaystyle T = 3a(a + b) = 3a(4a) = 1200\), ahonnan \(\displaystyle a^{2} = 100\), \(\displaystyle a = 10\) és \(\displaystyle b = 30\). A kerülete ekkor \(\displaystyle 2(10 + 30 + 3\cdot10) = 140\) cm.
A második elrendezésben \(\displaystyle d = 2c\), \(\displaystyle T = 2c(2c+d) = 2c(4c) = 1200\), ahonnan \(\displaystyle 8c^{2} = 1200\), \(\displaystyle c^{2} = 150\), \(\displaystyle c = 5 \sqrt 6\) és \(\displaystyle d = 10 \sqrt 6\). A kerülete ekkor \(\displaystyle 2\big(2\cdot 5 \sqrt 6 + 10 \sqrt 6 + 10 \sqrt 6 \big) = 60 \sqrt 6\) cm.
Statisztika:
161 dolgozat érkezett. 6 pontot kapott: 56 versenyző. 5 pontot kapott: 12 versenyző. 4 pontot kapott: 47 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 19 versenyző. Nem versenyszerű: 4 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 11 dolgozat.
A KöMaL 2019. szeptemberi matematika feladatai

