 |
A K. 691. feladat (2021. március) |
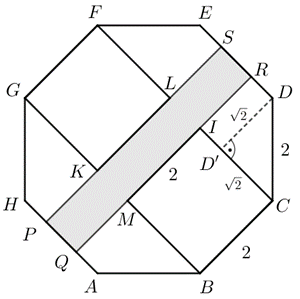
K. 691. Az \(\displaystyle ABCDEFGH\) szabályos nyolcszög 2 egység hosszú \(\displaystyle BC\) és \(\displaystyle GF\) oldalára befelé a \(\displaystyle BCIM\) és az \(\displaystyle FGKL\) négyzetet rajzoljuk. Mekkora a területe annak a téglalapnak, amelyet az \(\displaystyle AH\), \(\displaystyle KL\), \(\displaystyle ED\) és \(\displaystyle IM\) egyenesek határolnak?
(6 pont)
A beküldési határidő 2021. április 12-én LEJÁRT.
Megoldás: Állítsunk merőlegest \(\displaystyle D\)-ből \(\displaystyle CI\)-re. \(\displaystyle DCD'\angle 45^{\circ}\) . Így a Pitagorasz-tétel miatt \(\displaystyle DD' = D'C = \sqrt 2 \). A \(\displaystyle PQRS\) téglalap \(\displaystyle QR\) oldalának hossza \(\displaystyle 2\sqrt 2 +2\).
\(\displaystyle ID' = 2-\sqrt 2 \). \(\displaystyle SR = 2-2RD = 2-2(2-\sqrt 2 ) = 2\sqrt 2-2\).
A \(\displaystyle PQRS\) téglalap területe: \(\displaystyle (2\sqrt 2 +2)(2\sqrt 2 -2)=8-4=4\).
Statisztika:
| 83 dolgozat érkezett. |
| 6 pontot kapott: | Bacsek Emma Borbála, Baksa Anna, Barta Veronika, Biró Anna, Biró Róza, Boros Helga Dóra, Bottyán Márton Péter, Buday Noémi, Csóka Péter, Dancsák Dénes, Divényi Bernadett, Dukát Levente, Érdi Ferenc Vince, Ferencsik Zsombor, Fodor Gergely, Fórizs Borbála, Fórizs Emma, Gulyás Janka, Gyönki Dominik, Heim Flóra, Hochenburger Zoárd, Horváth 221 Zsóka, Jenei Ákos Zoltán, Kéki Edit, Klusóczki-Bogdándi Alma, Kornya Gergely Csaba, Kuba Nikoletta, Kurucz Kitti, Laczó Dávid, Laskai Botond, Lehoczky Örs Hunor, Lupkovics Lilla, Mayer Krisztián, Mészáros Ádám, Molnár Kristóf, Richlik Márton, Sándor Eszter, Schäffer Donát, Sebestyén József Tas, Simon Géza, Solymosi Csongor, Susán Henrik, Szabó Csenge, Szeibert Dominik, Yang Yu jie. |
| 5 pontot kapott: | 23 versenyző. |
| 4 pontot kapott: | 1 versenyző. |
| 3 pontot kapott: | 3 versenyző. |
| 2 pontot kapott: | 1 versenyző. |
| 1 pontot kapott: | 3 versenyző. |
| 0 pontot kapott: | 4 versenyző. |
| Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: | 3 dolgozat. |
A KöMaL 2021. márciusi matematika feladatai



