 Problem K. 87. (September 2006)
Problem K. 87. (September 2006)
K. 87. The growth of an isosceles Pythagoras tree has the following pattern: In the first year, the tree grows its trunk, which is a square. In the second year, an isosceles right-angled triangle grows on top, such that its hypotenuse is the top side of the square, and then the first two branches, also square in shape, grow from the legs of the triangle. Then this pattern repeats every year, that is, an isosceles right triangle grows on the top of each branch and its legs grow two new square branches. Given that the trunk (i.e. the first square) is 8 metres wide, calculate the height and the width of the tree at the end of the fourth year. (Hint: Draw a diagram of the tree to scale on squared paper. Let one little square represent 2 metres.)
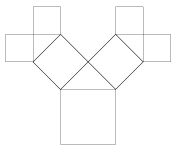
(6 pont)
Deadline expired on October 10, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: A négyzetek az átlóik behúzásával a rájuk kerülő egyenlőszárú derékszögű háromszögekkel egybevágó háromszögekre bonthatók, így könnyen számíthatók a kért adatok, a fa magassága 8+4+4+4+4=24 méter, szélessége 2.(4+4+4+4)=32 méter.
(A fával a következő internetes oldalon lehet játszani: http://www.ies.co.jp/math/java/geo/pytreea/pytreea.html )
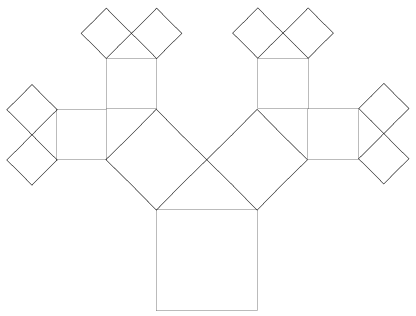
Statistics:
312 students sent a solution. 6 points: 102 students. 5 points: 7 students. 4 points: 29 students. 3 points: 58 students. 2 points: 14 students. 1 point: 5 students. 0 point: 87 students. Unfair, not evaluated: 10 solutionss.
Problems in Mathematics of KöMaL, September 2006
