Problem M. 382. (December 2018)

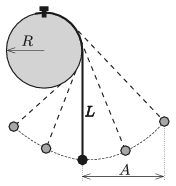
M. 382. One end of a thin, flexible and not stretchable thread is attached to the topmost point on the rim of a cylinder of radius \(\displaystyle R\). The cylinder is fixed and it has a horizontal axis. A small object is attached to the other end of the thread. In the equilibrium position the vertical part of the thread has a length of \(\displaystyle L=3R\). The object is displaced, as shown in the figure, and then it is released. The period of the motion – for a relatively large initial displacement – of the object depends on the ''amplitude'' \(\displaystyle A\). Measure for several different values of \(\displaystyle A\) by what percent the period of this pendulum \(\displaystyle T(A)\) differs from the period \(\displaystyle T_0=2\pi\sqrt{{L}/{g}}\) of a simple pendulum of length \(\displaystyle L\)?

(6 pont)

Deadline expired on January 10, 2019.

Statistics:

11 students sent a solution.
6 points:	Kondákor Márk, Kozák 023 Áron, Olosz Adél, Pácsonyi Péter.
5 points:	Fülöp Sámuel Sihombing, Morvai Orsolya, Varga 235 Áron.
4 points:	2 students.
3 points:	2 students.

Problems in Physics of KöMaL, December 2018