 Problem P. 4373. (October 2011)
Problem P. 4373. (October 2011)
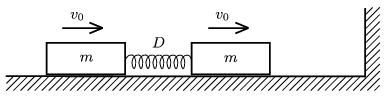
P. 4373. Bodies of mass m=0.5 kg, resting on a horizontal frictionless tabletop, are connected with an unstretched spring of length L=20 cm, and of spring constant D=16 N/m. The mass of the spring is negligible. At a certain moment the bodies are given an initial speed of v0=0.36 m/s, towards the wall on the right. The body at the right collides with the wall totally elastically.
a) What is the greatest compression of the spring during the motion?
b) After the collision with the wall how much time elapses until the moment when the bodies are the closest?
c) Will there be any other collision with the wall later? How will the system of bodies move if a long enough time elapses? d) What is the change in the linear momentum of the system after all collisions occurred?
(4 pont)
Deadline expired on November 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) 9 cm.
\(\displaystyle b)\) \(\displaystyle T/4\approx 0{,}2~\) s.
\(\displaystyle c)\) A jobb oldali test még egyszer ütközik a fallal; utána a rugó nyújtatlan állapotú marad, és mindkét test \(\displaystyle v_{0}\) sebességgel fog mozogni balra.
\(\displaystyle d)\) \(\displaystyle \Delta I= 0{,}72~\textrm{kg}{\textrm{m}\over \textrm{s}}\).
Statistics:
110 students sent a solution. 4 points: Antalicz Balázs, Bolgár Dániel, Csáky Pál, Csathó Botond, Czigány Máté Gábor, Czipó Bence, Emri Tamás, Ferenczi András, Fonyó Viktória, Garami Anna, Havasi 0 Márton, Horicsányi Attila, Horváth András Levente, Jenei Márk, Kollarics Sándor, Koncz Gabriella, Kovács 444 Áron, Kovács Ágnes, Mázik László, Morvay Bálint, Öreg Zsombor, Papp Roland, Park Choong Eun, Sárvári Péter, Seres Imre, Simig Dániel, Sisák Mária Anna, Szabó 928 Attila, Székely Eszter, Szélig Áron, Szigeti Bertalan György, Tilk Bence, Tóth Balázs, Ürge László, Vajda Balázs. 3 points: 37 students. 2 points: 24 students. 1 point: 12 students. Unfair, not evaluated: 2 solutionss.
Problems in Physics of KöMaL, October 2011
