Problem P. 4653. (September 2014)

P. 4653. There is a small (point-like) object at the topmost point of a fixed sphere of absolutely smooth surface. If this object is slightly displaced from its equilibrium position it slides frictionlessly along the surface of the sphere for a while, and then leaving the sphere it falls down.

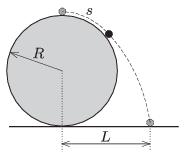
\(\displaystyle a)\) How much distance is covered by the small object along the surface of the sphere until it leaves the sphere?

\(\displaystyle b)\) Measured from the vertical diameter of the sphere, at what distance \(\displaystyle L\) will the object hit the horizontal surface?

The radius of the sphere is \(\displaystyle R=1.5\) m.

(4 pont)

Deadline expired on October 10, 2014.

Statistics:

105 students sent a solution.
4 points:	73 students.
3 points:	14 students.
2 points:	9 students.
1 point:	2 students.
0 point:	7 students.

Problems in Physics of KöMaL, September 2014