 Problem P. 4921. (March 2017)
Problem P. 4921. (March 2017)
P. 4921. Frictionless movable pistons are in a horizontal cylinder, closed at both ends, and confine samples of diatomic, ideal gas of the same type and of the same volume of \(\displaystyle V_0=2~\rm dm^3\) at a pressure of \(\displaystyle p_0=10^4\) Pa, and at the same temperature. The pistons are connected by a spring the length of which when it is not compressed or stretched is the same as the length of the cylinder. Between the pistons there is vacuum.
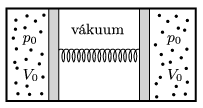
\(\displaystyle a)\) What is the energy stored in the spring in its compressed position described above?
\(\displaystyle b)\) The gas samples are heated slowly in the same way, and their absolute temperature is tripled. What will the pressure of the gas samples be at the end of the heating process?
\(\displaystyle c)\) How much heat was added to the system, if the losses are neglected?
(5 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Legyen a dugattyúk keresztmetszete \(\displaystyle A\), akkor mindkét dugattyú \(\displaystyle x=V_0/A\) távol van a henger közelebbi végétől. Ha a rugó rugóállandója \(\displaystyle D\), akkor \(\displaystyle 2x\) összenyomódás mellett
\(\displaystyle 2\frac{V_0}{A}D=p_0A\)
erőt fejt ki a dugattyúkra. Eszerint a rugóállandó
\(\displaystyle D=\frac{p_0 A^2}{2V_0}. \)
A rugóban tárolt rugalmas energia ebben az állapotban
\(\displaystyle W=\frac{1}{2}D(2x)^2=\frac{1}{2}D\left(2\frac{V_0}{A}\right)^2=p_0V_0=20~\rm J. \)
\(\displaystyle b)\) Ha a melegítés hatására a gázok térfogata \(\displaystyle V_1\)-re, a nyomásuk \(\displaystyle p_1\)-re, a rugó összenyomódása pedig \(\displaystyle 2x_1=2\frac{V_1}{A}\)-ra nő, a dugattyúkra ható erők egyensúlyának feltétele:
\(\displaystyle p_1A=2D\frac{V_1}{A},\)
amit a kezdeti állapot egyensúlyi egyenletével összevetve kapjuk, hogy
\(\displaystyle V_1 =\frac{p_1}{p_0}V_0.\)
Másrészt a gáztörvény szerint
\(\displaystyle p_1V_1= \frac{p_1^2}{p_0}V_0 =3p_0V_0,\)
és így
\(\displaystyle p_1=\sqrt{3}p_0=1{,}73\cdot10^4~\rm Pa.\)
\(\displaystyle c)\) A gázokkal közölt hő az I. főtétel szerint
\(\displaystyle Q=\Delta E_\text{belső}+\Delta W_\text{rugó}=2\cdot \frac{5}{2}\left(p_1V_1-p_0V_0\right)+p_1V_1-p_0V_0=12\,p_0V_0=240~\rm J.\)
Statistics:
61 students sent a solution. 5 points: Balog 518 Lóránd, Bekes Nándor, Bíró Dániel, Bukor Benedek, Csire Roland, Csuha Boglárka, Édes Lili, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Guba Zoltán, Illés Gergely, Klučka Vivien, Kondákor Márk, Kozák András, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Pszota Máté, Sal Dávid, Tófalusi Ádám, Tóth 111 Máté , Zöllner András. 4 points: Bartók Imre, Debreczeni Tibor, Fekete Balázs Attila, Jáger Balázs, Kolontári Péter, Magyar Róbert Attila, Nagy 555 Botond, Németh 123 Balázs, Páhoki Tamás, Richlik Róbert, Szakály Marcell, Szentivánszki Soma , Turcsányi Ádám, Varga-Umbrich Eszter. 3 points: 14 students. 2 points: 3 students. 1 point: 1 student. 0 point: 2 students.
Problems in Physics of KöMaL, March 2017
