 Problem P. 4951. (September 2017)
Problem P. 4951. (September 2017)
P. 4951. Approximately by what distance does the Earth's path diverges from the straight line in one second, during its revolution around the Sun?
(4 pont)
Deadline expired on October 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ismert, hogy a Nap-Föld távolság
\(\displaystyle R=1~\text{csillagászati egység} =1~{\rm CsE}= 150~\text{millió km}.\)
A jó közelítéssel kör alakú pálya \(\displaystyle 2R\pi\) hosszú kerületét 1 év alatt teszi meg a Föld, sebessége tehát
\(\displaystyle v=2R\pi/T=30~\rm km/s.\)
A Föld \(\displaystyle t=1\) másodperc alatt \(\displaystyle x=vt=30~\)km-t tesz meg, miközben egy kicsit eltér a kör érintőjétől (vagyis az egyenes iránytól). Az eltérést többféle módon is kiszámíthatjuk.
\(\displaystyle (i)\) Ha egyenesen haladna a Föld, \(\displaystyle x\) elmozdulás után \(\displaystyle \sqrt{R^2+x^2}\) távol kerülne a Naptól, de a körpályán a távolsága ténylegesen \(\displaystyle R\) marad. Az eltérés nagysága
\(\displaystyle \Delta R=\sqrt{R^2+x^2}-R= \sqrt{150\,000\,000^2+30^2}-150\,000\,000.\)
Sajnos ezt a mennyiséget közvetlen számolással nem tudjuk kiszámítani, mert a négyzetgyök értéke a zsebszámológépek pontossága erejéig éppen 1 CsE, tehát az eltérés numerikusan nullának adódik.
Ügyesebben is eljárhatunk, ha a keresett mennyiséget megszorozzuk és el is osztjuk egy megfelelően választott kifejezéssel:
\(\displaystyle \Delta R=\frac{\left(\sqrt{R^2+x^2}-R\right)\cdot \left(\sqrt{R^2+x^2}+R\right)}{\left(\sqrt{R^2+x^2}+R\right)}.\)
A számláló \(\displaystyle (R^2+x^2)-R^2=x^2,\) a nevező pedig jó közelítéssel \(\displaystyle 2R\), az eltérés tehát
\(\displaystyle \Delta R\approx \frac{x^2}{2R}=\frac{(30~\rm km)^2}{3\cdot 10^6~\rm km}=3~\rm mm.\)
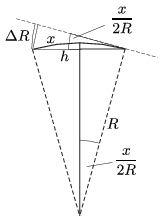
\(\displaystyle (ii)\) Geometriai megfontolásokkal is megkaphatjuk a keresett távolságot. A Föld \(\displaystyle x\) hosszúságú elmozdulása során a Föld jó közelítéssel \(\displaystyle x\) távolságra kerül az eredeti helyzetétől (ha a húr \(\displaystyle h\) hosszát a körív \(\displaystyle x\) hosszával közelítjük). Ezalatt a Földet a Nappal összekötő egyenes \(\displaystyle x/R\) szöggel fordul el, a kör érintője tehát a kiindulási pontban \(\displaystyle x/(2R)\) szöget zár be a kör húrjával. Így a Föld eltávolodása az érintő egyenesétől (az egyenesen mért távolságot az \(\displaystyle x\) sugarú, \(\displaystyle x/(2R)\) középponti szögű körív hosszával közelítve):
\(\displaystyle \Delta R\approx \frac{x^2}{2R}=3~\rm mm.\)
\(\displaystyle (iii)\) Az eltérést a Föld centripetális gyorsulásából is kiszámíthatjuk. A \(\displaystyle v\) sebességgel mozgó Föld \(\displaystyle a=v^2/R\) gyorsulással ,,esik'' a Nap felé, \(\displaystyle t=1~\)s alatt tehát
\(\displaystyle \Delta R=\frac{a}{2}t^2=\frac{v^2}{2R}t^2=\frac{x^2}{2R}=3~\rm mm\)
távol kerül a kört érintő egyenestől.
Statistics:
80 students sent a solution. 4 points: Balaskó Dominik, Bálint Boglárka Eszter, Békési Ábel, Bukor Benedek, Cseh Noémi, Fekete András Albert, Fekete Balázs Attila, Garamvölgyi István Attila, Geretovszky Anna, Guba Zoltán, Hajnal Dániel Konrád, Hervay Bence, Jánosdeák Márk, Kolontári Péter, Kovács 111 Bence, Kozák 023 Áron, Lipták Gergő, Markó Gábor, Marozsák Tádé, Merkl Gergely, Merkl Levente, Morvai Orsolya, Ónodi Gergely, Pácsonyi Péter, Paulovics Péter, Pénzes Ádám, Rozgonyi Gergely, Rusvai Miklós, Selmi Bálint, Szabó 314 László, Szakály Marcell, Tafferner Zoltán, Tóth 111 Máté , Turcsányi Ádám, Veres Kristóf, Viczián Anna, Vígh Márton. 3 points: Andorfi István, Balog 518 Lóránd, Édes Lili, Forczek Bianka, Jánosik Áron, Kálóczi Kornél, Kiss Dániel Márk, Magyar Máté, Takács Nóra, Tófalusi Ádám, Turcsányi Máté. 2 points: 15 students. 1 point: 9 students. 0 point: 6 students. Unfair, not evaluated: 2 solutionss.
Problems in Physics of KöMaL, September 2017
