 |
A P. 4954. feladat (2017. szeptember) |
P. 4954. Egy viszonylag nagy tömegű méterrúd egyik vége egy vízszintes helyzetű tengely körül szabadon elfordulhat. A kezdetben vízszintes rúdra tegyünk egyenlő, 10 cm-es távolságokban 5 Ft-os pénzérméket, összesen 11 darabot.
\(\displaystyle a)\) Mi történik a pénzérmékkel nagyon rövid idővel az elengedés pillanata után?
\(\displaystyle b)\) Mely érmék nem mozdulnak meg a rúdhoz képest, amikor a rúd az eredeti helyzetével már 10\(\displaystyle {}^\circ\)-ot zár be?
A pénzérmék és a méterrúd közötti tapadó súrlódás együtthatója 0,5.
Budó Ágoston Fizikai Feladatmegoldó Verseny, Szeged
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. Számítsuk ki az \(\displaystyle m\) tömegű és \(\displaystyle L=1\) m hosszúságú rúd \(\displaystyle \omega\) szögsebességét és \(\displaystyle \beta\) szöggyorsulását abban (az 1. ábrán látható) helyzetben, amikor az elfordulása az eredeti helyzetéhez képest \(\displaystyle \varphi\).
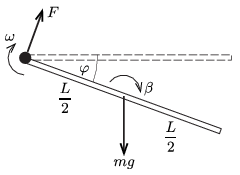
1. ábra
Ha a tengelynél ható erőnek a rúdra merőleges komponense \(\displaystyle F\), akkor a forgómozgás alapegyenlete szerint
\(\displaystyle F\frac{L}{2}=\frac{1}{12}mL^2\beta,\)
a tömegközéppont mozgásegyenlete pedig (a rúdra merőleges irányban):
\(\displaystyle mg\cos\varphi-F=m\frac{L}{2}\beta.\)
Ezekből \(\displaystyle F\) kiküszöbölése után
\(\displaystyle \beta=\frac{3g}{2L}\cos\varphi\)
adódik. (A rúd viszonylag nagy tömege miatt a pénzérmék tehetetlenségi nyomatékát és a pénzérmék által a rúdra kifejtett erőket nem vettük figyelembe.)
A rúd szögsebessége az energiamegmaradás törvényét alkalmazva határozható meg.
\(\displaystyle mg\frac{L}{2}\sin\varphi=\frac{mL^2}{3}\,\frac{\omega^2}{2},\)
vagyis
\(\displaystyle \omega^2=\frac{3g}{L}\sin\varphi.\)
Megjegyzés. A szögsebesség négyzetét megadó egyenletből (annak mindkét oldalát az idő szerint deriválva) közvetlenül is megkaphatjuk a szöggyorsulát.
Tekintsük azt a pénzérmét, amelyik a tengelytől \(\displaystyle x\) távolságra helyezkedik el, és számítsuk ki, mekkora \(\displaystyle N\) nyomóerőt és mekkora \(\displaystyle S\) súrlódási erőt fejt ki rá a rúd a \(\displaystyle \varphi\) szögű helyzetben (2. ábra). (Legyen a pénzérme tömege \(\displaystyle m_0\), mérete a rúd méretéhez képest elhanyagolható.)
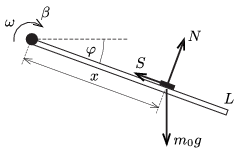
2. ábra
A pénzérmére felírható mozgásegyenletek (a korábban kiszámított \(\displaystyle \beta\) és \(\displaystyle \omega^2\) felhasználásával:
\(\displaystyle m_0g\cos\varphi-N=mx\beta, \qquad S-m_0g\sin\varphi=mx\omega^2,\)
ahonnan
\(\displaystyle N(\varphi)=m_0g\cos\varphi\left(1-\frac{3x}{2L}\right),\)
\(\displaystyle S(\varphi)=m_0g\sin\varphi\left(1+\frac{3x}{L}\right).\)
A pénzérmék csak akkor mozoghatnak a fentebb leírt módon, ha \(\displaystyle S\le \mu N\), ellenkező esetben a pénzérme megcsúszik a rúdon, illetve ha \(\displaystyle N\ge 0\), ellenkező esetben a pénz elválik a rúdtól, lerepül róla.
\(\displaystyle a)\) Az indulás pillanatában \(\displaystyle \varphi=0\), tehát \(\displaystyle S=0\) és \(\displaystyle N=m_0g\left(1-\frac{3x}{2L}\right).\) Ezek szerint egyik pénz sem csúszik el a rúdon, viszont azok, amelyekre \(\displaystyle x>\tfrac{2}{3}L\approx 67\) cm, vagyis a 70, 80, 90 és 100 centiméteres jelekhez tett 5 forintosok eltávolodnak a rúdtól, lerepülnek arról.
\(\displaystyle b)\) A \(\displaystyle \varphi=10^\circ\)-os helyzetben azok a pénzek nem csúsznak meg, amelyekre
\(\displaystyle \frac{S}{N}=\tg10^\circ\,\frac{2L+6x}{2L-3x}\le 0{,}5;\)
azaz \(\displaystyle x\le 0{,}25\) m. Tehát csak a forgástengelynél, illetve a 10 és a 20 cm-es jeleknél elhelyezett 5 forintosok maradhatnak a rúdon eddig az elfordulásig, a többiek már korábban megcsúsztak a méterrúdon.
Statisztika:
52 dolgozat érkezett. 5 pontot kapott: Bartók Imre, Békési Ábel, Berke Martin, Bíró Dániel, Bukor Benedek, Csire Roland, Elek Péter, Guba Zoltán, Jánosdeák Márk, Kiss Dániel Márk, Magyar Róbert Attila, Makovsky Mihály, Marozsák Tóbiás , Morvai Orsolya, Olosz Adél, Sal Dávid, Tófalusi Ádám. 4 pontot kapott: Illés Gergely, Molnár Mátyás. 3 pontot kapott: 17 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. szeptemberi fizika feladatai

