Problem P. 4954. (September 2017)

P. 4954. One end of a metre stick, which has fairly big mass, can be rotated freely about a horizontal axle. Put 11 five-forint coins onto the initially horizontal stick at a distance of 10 cm from each other.

\(\displaystyle a)\) What happens to the coins right after the moment when the stick was released?

\(\displaystyle b)\) Which coins do not move with respect to the stick at the moment when the stick encloses an angle of 10\(\displaystyle {}^\circ\) with its original position? The coefficient of static friction between the stick and the coins is 0.5.

(5 pont)

Deadline expired on October 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Számítsuk ki az \(\displaystyle m\) tömegű és \(\displaystyle L=1\) m hosszúságú rúd \(\displaystyle \omega\) szögsebességét és \(\displaystyle \beta\) szöggyorsulását abban (az 1. ábrán látható) helyzetben, amikor az elfordulása az eredeti helyzetéhez képest \(\displaystyle \varphi\).

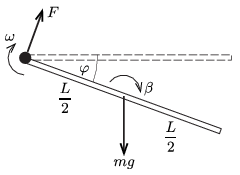
1. ábra

Ha a tengelynél ható erőnek a rúdra merőleges komponense \(\displaystyle F\), akkor a forgómozgás alapegyenlete szerint

\(\displaystyle F\frac{L}{2}=\frac{1}{12}mL^2\beta,\)

a tömegközéppont mozgásegyenlete pedig (a rúdra merőleges irányban):

\(\displaystyle mg\cos\varphi-F=m\frac{L}{2}\beta.\)

Ezekből \(\displaystyle F\) kiküszöbölése után

\(\displaystyle \beta=\frac{3g}{2L}\cos\varphi\)

adódik. (A rúd viszonylag nagy tömege miatt a pénzérmék tehetetlenségi nyomatékát és a pénzérmék által a rúdra kifejtett erőket nem vettük figyelembe.)

A rúd szögsebessége az energiamegmaradás törvényét alkalmazva határozható meg.

\(\displaystyle mg\frac{L}{2}\sin\varphi=\frac{mL^2}{3}\,\frac{\omega^2}{2},\)

vagyis

\(\displaystyle \omega^2=\frac{3g}{L}\sin\varphi.\)

Megjegyzés. A szögsebesség négyzetét megadó egyenletből (annak mindkét oldalát az idő szerint deriválva) közvetlenül is megkaphatjuk a szöggyorsulát.

Tekintsük azt a pénzérmét, amelyik a tengelytől \(\displaystyle x\) távolságra helyezkedik el, és számítsuk ki, mekkora \(\displaystyle N\) nyomóerőt és mekkora \(\displaystyle S\) súrlódási erőt fejt ki rá a rúd a \(\displaystyle \varphi\) szögű helyzetben (2. ábra). (Legyen a pénzérme tömege \(\displaystyle m_0\), mérete a rúd méretéhez képest elhanyagolható.)

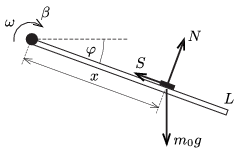
2. ábra

A pénzérmére felírható mozgásegyenletek (a korábban kiszámított \(\displaystyle \beta\) és \(\displaystyle \omega^2\) felhasználásával:

\(\displaystyle m_0g\cos\varphi-N=mx\beta, \qquad S-m_0g\sin\varphi=mx\omega^2,\)

ahonnan

\(\displaystyle N(\varphi)=m_0g\cos\varphi\left(1-\frac{3x}{2L}\right),\)

\(\displaystyle S(\varphi)=m_0g\sin\varphi\left(1+\frac{3x}{L}\right).\)

A pénzérmék csak akkor mozoghatnak a fentebb leírt módon, ha \(\displaystyle S\le \mu N\), ellenkező esetben a pénzérme megcsúszik a rúdon, illetve ha \(\displaystyle N\ge 0\), ellenkező esetben a pénz elválik a rúdtól, lerepül róla.

\(\displaystyle a)\) Az indulás pillanatában \(\displaystyle \varphi=0\), tehát \(\displaystyle S=0\) és \(\displaystyle N=m_0g\left(1-\frac{3x}{2L}\right).\) Ezek szerint egyik pénz sem csúszik el a rúdon, viszont azok, amelyekre \(\displaystyle x>\tfrac{2}{3}L\approx 67\) cm, vagyis a 70, 80, 90 és 100 centiméteres jelekhez tett 5 forintosok eltávolodnak a rúdtól, lerepülnek arról.

\(\displaystyle b)\) A \(\displaystyle \varphi=10^\circ\)-os helyzetben azok a pénzek nem csúsznak meg, amelyekre

\(\displaystyle \frac{S}{N}=\tg10^\circ\,\frac{2L+6x}{2L-3x}\le 0{,}5;\)

azaz \(\displaystyle x\le 0{,}25\) m. Tehát csak a forgástengelynél, illetve a 10 és a 20 cm-es jeleknél elhelyezett 5 forintosok maradhatnak a rúdon eddig az elfordulásig, a többiek már korábban megcsúsztak a méterrúdon.

Statistics:

52 students sent a solution.
5 points:	Bartók Imre, Békési Ábel, Berke Martin, Bíró Dániel, Bukor Benedek, Csire Roland, Elek Péter, Guba Zoltán, Jánosdeák Márk, Kiss Dániel Márk, Magyar Róbert Attila, Makovsky Mihály, Marozsák Tóbiás , Morvai Orsolya, Olosz Adél, Sal Dávid, Tófalusi Ádám.
4 points:	Illés Gergely, Molnár Mátyás.
3 points:	17 students.
2 points:	9 students.
1 point:	5 students.
0 point:	2 students.

Problems in Physics of KöMaL, September 2017