 |
A P. 4955. feladat (2017. szeptember) |
P. 4955. Két \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű, kis méretű golyó vízszintes síkban mozogva adott pillanatban \(\displaystyle d\) távolságra van egymástól. Ebben a pillanatban a sebességük \(\displaystyle v_0\), és a sebességvektorok az ábrán látható módon \(\displaystyle \alpha\) szöget zárnak be a golyókat összekötő egyenessel.
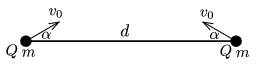
\(\displaystyle a)\) Milyen minimális távolságra közelíti meg egymást a két golyó?
\(\displaystyle b)\) Milyen nagy ekkor a sebességük?
Párkányi László Fizikaverseny, Pécs
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Írjuk le a golyók mozgását a tömegközéppontjukkal együtt mozgó koordináta-rendszerből. Ez a rendszer az eredeti vonatkoztatási rendszerhez képest \(\displaystyle v_0\sin\alpha\) sebességgel mozog a golyókat összekötő egyenesre merőleges irányban.
A tömegközépponti rendszerben kezdetben mindkét test \(\displaystyle v_0\cos\alpha\) sebességgel mozog a másik felé. Amikor a legközelebb, valamekkora \(\displaystyle d_0\) távolságra vannak egymáshoz, a sebességük éppen nulla. Felírhatjuk az energia megmaradását kifejező egyenletet:
\(\displaystyle 2\cdot \frac{1}{2}m(v_0\cos\alpha)^2+\frac{kQ^2}{d}=\frac{kQ^2}{d_0},\)
ahonnan a minimális távolság
\(\displaystyle d_0=\frac{kQ^2d}{kQ^2+mv_0^2d\cos^2\alpha}.\)
\(\displaystyle b)\) Amikor a két golyó a legjobban megközelítette egymást, sebességük a tömegközépponti rendszerben nulla, az eredeti koordináta-rendszerben pedig \(\displaystyle v_0\sin\alpha\).
Statisztika:
79 dolgozat érkezett. 5 pontot kapott: An Tamás, Bartók Imre, Békési Ábel, Csire Roland, Debreczeni Tibor, Fekete Balázs Attila, Geretovszky Anna, Guba Zoltán, Kiszli Zalán, Kolontári Péter, Kondákor Márk, Makovsky Mihály, Marozsák Tádé, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Póta Balázs, Sal Dávid, Shirsha Bose, Tófalusi Ádám, Tóth 111 Máté , Turcsányi Ádám, Varga 666 Róbert Zoltán. 4 pontot kapott: 34 versenyző. 3 pontot kapott: 11 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 8 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. szeptemberi fizika feladatai

