 Problem P. 4957. (September 2017)
Problem P. 4957. (September 2017)
P. 4957. The sides of a square-shaped frame, shown in the figure are made of wires of resistances \(\displaystyle r_1\) and \(\displaystyle r_2\). The frame is in uniform magnetic field, which is perpendicular to the plane of the figure and is increasing at a constant rate. What should the resistance \(\displaystyle R\) of the wire connected across the diagonal of the frame be, in order that this wire is warmed up at the greatest rate?
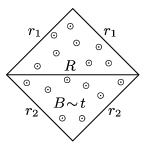
(5 pont)
Deadline expired on October 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A változó mágneses tér miatt az ábrán látható mindkét háromszög oldalai mentén ugyanakkora \(\displaystyle U_0\) körfeszültség indukálódik.
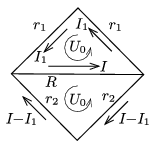
Az ábrán látható jelölésekkel a Kirchhoff-féle huroktörvény egyenletei:
\(\displaystyle RI+2r_1I_1=U_0,\)
\(\displaystyle RI+ 2r_2(I-I_1) =-U_0.\)
Ezekből következik, hogy
\(\displaystyle I=U_0\frac{r_1-r_2}{R(r_1+r_2)+2r_1r_2},\)
az \(\displaystyle R\) ellenállás melegedésének hőteljesítménye:
\(\displaystyle P=I^2R= R\left(U_0\frac{r_1-r_2}{R(r_1+r_2)+2r_1r_2}\right)^2.\)
Ennek a kifejezésnek keressük a maximumát \(\displaystyle R\) függvényében. Mivel \(\displaystyle P(R)\) reciproka így írható fel:
\(\displaystyle \frac{1}{P(R)}=\text{állandó}\cdot \left( R(r_1+r_2)^2+\frac{(2r_1r_2)^2}{R}+\text{állandó}\right),\)
a leggyorsabb melegedés annál az ellenállásnál következik be, amelyre
\(\displaystyle R(r_1+r_2)^2+\frac{(2r_1r_2)^2}{R}\)
minimális. Alkalmazva a számtani és mértani közepekre vonatkozó egyenlőtlenséget azt kapjuk, a \(\displaystyle P(R)\) függvény a maximumát az
\(\displaystyle R=\frac{2r_1r_2}{r_1+r_2}\)
értéknél veszi fel. Ezek szerint akkor melegszik a leggyorsabban a négyzet átlójában található ellenálláshuzal, ha \(\displaystyle R\) az \(\displaystyle r_1\) és \(\displaystyle r_2\) ellenállások harmonikus középértéke.
Statistics:
14 students sent a solution. 5 points: Bíró Dániel, Elek Péter, Fekete Balázs Attila, Kondákor Márk, Marozsák Tóbiás , Olosz Adél, Sal Dávid, Shirsha Bose, Tófalusi Ádám. 4 points: Berke Martin. 3 points: 1 student. 2 points: 1 student. 0 point: 2 students.
Problems in Physics of KöMaL, September 2017
