Problem P. 4964. (October 2017)

P. 4964. What is the least force with which an ice cube sliding on ice can be turned over? (Friction is negligible.)

(5 pont)

Deadline expired on November 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a jégkocka oldaléle \(\displaystyle d\) hosszú, tömege \(\displaystyle m\) és hasson a jégkockára az egyik oldaléle középpontjában \(\displaystyle F\) nagyságú, a vízszintessel \(\displaystyle \alpha\) szöget bezáró erő (lásd az ábrát).

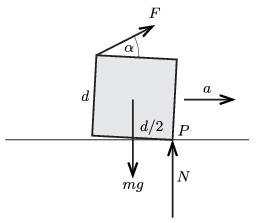
A felborulás határhelyzetében a kocka már egy kicsit megemelkedik, és csak a \(\displaystyle P\) ponton átmenő élénél érintkezik a vízszintes jégfelülettel. A kocka vízszintes irányban egyenletesen gyorsul, a függőleges gyorsulása és a forgási szöggyorsulása nulla. A mozgásegyenletek ennek megfelelően:

\(\displaystyle F\cos\alpha=ma,\)

\(\displaystyle F\sin\alpha+N-mg=0,\)

\(\displaystyle F\frac{d}{2}\cos\alpha+F\frac{d}{2}\sin\alpha-N\frac{d}{2}=0.\)

(A forgómozgás alapegyenletét a tömegközéppontra írtuk fel. Vigyázat: más pontra felírt forgási egyenlet rossz eredményre vezethet!)

A fenti egyenletekből az erőre az

\(\displaystyle F=\frac{1}{\cos\alpha+2\sin\alpha}mg\)

kifejezés adódik. Ennek legkisebb értéke a nevező maximumához tartozik. Belátható (egy 1 és 2 oldalélű, \(\displaystyle \alpha\) szögben megbillentett téglalap legmagasabb pontjának megkeresésével, vagy trigonometrikus átalakításokkal, esetleg differenciálszámítással), hogy

\(\displaystyle \cos\alpha+2\sin\alpha\le \sqrt{5},\)

és a szélsőérték \(\displaystyle \tg\alpha=2\), vagyis \(\displaystyle \alpha\approx63^\circ\) szöghöz tartozik.

A jégkockát tehát a súlyának \(\displaystyle 1/\sqrt{5}\) részével, annak kb. 45%-ával lehet felborítani.

Statistics:

59 students sent a solution.
5 points:	Bartók Imre, Csire Roland, Elek Péter, Fekete Balázs Attila, Guba Zoltán, Jánosik Áron, Kolontári Péter, Kozák András, Marozsák Tóbiás , Olosz Adél, Póta Balázs, Sal Dávid, Tófalusi Ádám.
4 points:	Békési Ábel, Fajszi Bulcsú, Marozsák Tádé, Molnár Mátyás, Ónodi Gergely.
3 points:	16 students.
2 points:	15 students.
1 point:	2 students.
0 point:	4 students.
Unfair, not evaluated:	4 solutionss.

Problems in Physics of KöMaL, October 2017