 |
A P. 4971. feladat (2017. november) |
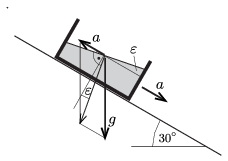
P. 4971. \(\displaystyle 30^\circ\)-os hajlásszögű, elég hosszú lejtőn gyorsulva csúszik lefelé egy vízzel félig telt tartály. Mekkora szöget zár be a víz felszíne a lejtő síkjával, ha a tartály és a lejtő közötti súrlódási együttható 0,2?
Példatári feladat alapján
(4 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. A tartály (és vele együtt a víz) \(\displaystyle a=g(\sin30^\circ-0{,}2\cos30^\circ)= 0{,}33\,g\) gyorsulással mozog a lejtőn lefelé. A tartállyal együtt mozgó, tehát gyorsuló koordináta-rendszerből szemlélve a rendszert, ott a valódi erők mellett fellépnek még a gyorsulással ellentétes irányú ,,tehetetlenségi erők'' is. Ezek nagysága \(\displaystyle ma\), ahol \(\displaystyle m\) a vizsgált test tömege. (Ilyen látszólagos erőknek tulajdonítjuk azt, hogy egy hirtelen fékező autóbuszban előre esünk, ha nem kapaszkodunk.)
A tehetetlenségi erő és a nehézségi erő lejtő irányú komponense (\(\displaystyle 0{,}5\,mg\)) együtt \(\displaystyle 0{,}17\,mg\), míg a nehézségi erő lejtőre merőleges komponense \(\displaystyle mg\cos30^\circ=0{,}87\,mg\).
A víz tehát ,,úgy érzi'', mintha a lejtőre merőleges iránnyal bizonyos \(\displaystyle \varepsilon\) szöget zárna be a nehézségi gyorsulás:
\(\displaystyle \tg\varepsilon =\frac{0{,}17\,g}{0{,}87\,g}, \qquad \varepsilon\approx 11^\circ.\)
A víz felszíne tehát (az állandósult állapot beállta után) a lejtő síkjával \(\displaystyle 11^\circ\)-os szöget fog bezárni.
Általában igaz, hogy \(\displaystyle \tg\varepsilon=\mu\), vagyis \(\displaystyle \varepsilon\) az ún. súrlódási határszöggel egyezik meg. Súrlódásmentes esetben \(\displaystyle \varepsilon=0\), vagyis a víz felszíne a lejtő síkjával párhuzamos (lásd a G. 615. gyakorlatot!). Amennyiben \(\displaystyle \mu=\tg\,30^\circ\), a tartály meg se indul a lejtőn, és ekkor a víz felszíne nyilván ,,vízszintes'', hiszen \(\displaystyle \varepsilon=30^\circ\).
Statisztika:
86 dolgozat érkezett. 4 pontot kapott: Balaskó Dominik, Beke Csongor, Berke Martin, Bonifert Balázs, Csire Roland, Csuha Boglárka, Édes Lili, Fekete András Albert, Fekete Balázs Attila, Guba Zoltán, Hajdu 046 Ákos, Hajnal Dániel Konrád, Horváth 999 Anikó, Illés Gergely, Jánosdeák Márk, Kiss 646 Mária, Kolontári Péter, Kovács Gergely Balázs, Kozák 023 Áron, Kozák András, Lipták Gergő, Magyar Máté, Markó Gábor, Marozsák Tóbiás , Máth Benedek, Merkl Gergely, Molnár 957 Barnabás, Molnár Mátyás, Morvai Orsolya, Németh Csaba Tibor, Olosz Adél, Pácsonyi Péter, Pszota Máté, Sal Dávid, Sas 202 Mór, Schrott Márton, Selmi Bálint, Szanda Márton, Tófalusi Ádám, Turcsányi Máté. 3 pontot kapott: 17 versenyző. 2 pontot kapott: 18 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. novemberi fizika feladatai

