 |
A P. 4981. feladat (2017. december) |
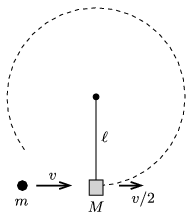
P. 4981. Egy \(\displaystyle m\) tömegű, \(\displaystyle v\) sebességű test az ábrán látható módon átlövi az \(\displaystyle M\) tömegű, felfüggesztett testet, amelyet \(\displaystyle v/2\) sebességgel hagy el. Először úgy, hogy az \(\displaystyle M\) tömegű test egy \(\displaystyle \ell\) hosszúságú, merev, elhanyagolható tömegű pálcán van felfüggesztve, másodszor pedig \(\displaystyle \ell\) hosszúságú fonálon lóg. Átlövése után az \(\displaystyle M\) tömegű test mindkét esetben befutja az \(\displaystyle \ell\) sugarú körpályát. Határozzuk meg az ehhez szükséges \(\displaystyle v\) sebességet mindkét esetben! Mekkora a két sebesség aránya?
Közli: Kobzos Ferenc, Dunaújváros
(4 pont)
A beküldési határidő 2018. január 10-én LEJÁRT.
Megoldás. A lendületmegmaradás miatt az \(\displaystyle M\) tömegű test sebessége az átlövése után
\(\displaystyle u=\frac{m}{M} \,\frac{v}2,\)
a pálya legmagasabb pontjában pedig (az energiamegmaradás törvénye szerint)
\(\displaystyle w=\sqrt{u^2-4g\ell}.\)
Ha az \(\displaystyle M\) tömegű test a fonálon függ, akkor a fonalat feszítő erő a pálya legmagasabb pontjánál
\(\displaystyle F=\frac{mw^2}{\ell}-mg\ge 0.\)
(Ha ez nem teljesülne, a fonál meglazulna). Innen következik, hogy
\(\displaystyle u \ge \sqrt{5\ell g},\)
azaz
\(\displaystyle v\ge\frac{2M}{m}\sqrt{5\ell g}=v_\text{fonál}.\)
Amikor az \(\displaystyle M\) tömegű test a merev pálcán függ, a pálcában nyomóerő is felléphet (\(\displaystyle F\) lehet negatív is). A körülfordulás feltétele most az, hogy a test sebessége még a pálya legmagasabb pontján se csökkenjen nullára, vagyis
\(\displaystyle w=\sqrt{u^2-4g\ell}>0,\)
azaz
\(\displaystyle u>\sqrt{4\ell g},\)
tehát
\(\displaystyle v\ge\frac{2M}{m}\sqrt{4\ell g}=v_\text{pálca} .\)
Leolvashatjuk, hogy az átforduláshoz szükséges sebességek aránya:
\(\displaystyle \frac{v_\text{fonál}}{v_\text{pálca}}=\sqrt{\frac{5}{4}}\approx 1{,}12.\)
Statisztika:
93 dolgozat érkezett. 4 pontot kapott: Andorfi István, Balaskó Dominik, Balog 518 Lóránd, Beke Csongor, Berke Martin, Bukor Benedek, Conrád Márk, Csuha Boglárka, Elek Péter, Fajszi Bulcsú, Fekete András Albert, Felföldi Gábor, Geretovszky Anna, Gulácsi Máté, Háder Márk István, Hajnal Dániel Konrád, Horváth 999 Anikó, Jánosdeák Márk, Kálóczi Kornél, Kiszli Zalán, Klučka Vivien, Kozák András, Lénárt Martin, Lipták Gergő, Magyar Máté, Magyar Róbert Attila, Máth Benedek, Merkl Gergely, Molnár 957 Barnabás, Morvai Orsolya, Olosz Adél, Pácsonyi Péter, Póta Balázs, Pszota Máté, Richlik Róbert, Sal Dávid, Sas 202 Mór, Selmi Bálint, Surján Botond, Szanda Márton, Tófalusi Ádám, Vass Bence, Vaszary Tamás, Viczián Anna, Zirci Márton. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 17 versenyző. 0 pontot kapott: 7 versenyző.
A KöMaL 2017. decemberi fizika feladatai

