 Problem P. 4983. (December 2017)
Problem P. 4983. (December 2017)
P. 4983. A cylinder, whose walls are thermally insulated, is attached to the inside part of the wall of a fixed closed cylinder as shown in the figure. The wall of the container is made of some heat conducting material. The thermally insulated piston of cross sectional area of 1 dm\(\displaystyle {}^2\) in the cylinder can move frictionlessly. Initially both in the container and in the cylinder there is a sample of air of volume 2.6 dm\(\displaystyle ^3\) at a pressure of \(\displaystyle 10^5\)Pa, and at a temperature of 27 \(\displaystyle {}^\circ\)C.
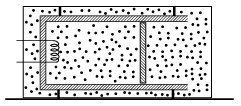
The air in the cylinder is then heated by means of an electric heater, while the temperature of the air in the container remains constant.
\(\displaystyle a)\) How much distance does the piston move if the temperature of the air in the cylinder increases to 77 \(\displaystyle {}^\circ\)C?
\(\displaystyle b)\) Sketch the change of states of the air inside the cylinder on the \(\displaystyle p\)–\(\displaystyle V\) diagram.
\(\displaystyle c)\) Estimate how much heat is absorbed by the air inside the cylinder.
(5 pont)
Deadline expired on January 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) A hengerben lévő gáz kezdeti adatait a szokásos módon \(\displaystyle p_0, V_0\) és \(\displaystyle T_0\)-lal jelöljük, a megváltozott értékeket pedig \(\displaystyle p, V\) és \(\displaystyle T\)-vel, a tartályban lévő levegő adatai ekkor: \(\displaystyle p, 2V_0-V\) és \(\displaystyle T_0\), hiszen a dugattyú két oldalán a nyomások megegyeznek, és az össztérfogat is állandó. Felírhatjuk az általános gáztörvényt mindkét levegőmennyiségre:
\(\displaystyle \frac{pV}{T}=\frac{p_0V_0}{T_0}, \qquad p(2V_0-V)=p_0V_0.\)
Innen kiszámítható, hogy
\(\displaystyle V=\frac{2T}{T-T_0}V_0=\frac{2\cdot 350}{350-300}\,2{,}6~{\rm dm}^3=2{,}8~{\rm dm}^3,\)
a hengerben lévő levegő térfogata 0,2 \(\displaystyle {\rm dm}^3\)-rel növekszik, vagyis a dugattyú 2 cm-rel mozdul el.
\(\displaystyle b)\) Az állapotváltozás a \(\displaystyle p-V\) diagramon a
\(\displaystyle p(V)=\frac{p_0V_0}{2V_0-V}\)
összefüggésnek megfelelően egy hiperbolával adható meg.
\(\displaystyle c)\) Az első főtétel szerint a felvett hő (kicsiny változások esetén)
\(\displaystyle Q=\Delta E+W'=\frac52\Delta(pV)+p\Delta V=\frac72p\Delta V+\frac52V\Delta p.\)
Mivel esetünkben \(\displaystyle p\) és \(\displaystyle V\) viszonylag keveset változik, a felvett hőt egyetlen lépésben kiszámíthatjuk (a képletben \(\displaystyle p\) és \(\displaystyle V\) helyébe a kezdeti és a megváltozott értékek számtani közepét helyettesíthetjük). Az így becsült érték: \(\displaystyle Q\approx 0{,}13\) kJ.
Statistics:
61 students sent a solution. 5 points: Andorfi István, Bíró Dániel, Bukor Benedek, Csire Roland, Csuha Boglárka, Elek Péter, Fajszi Bulcsú, Fekete Balázs Attila, Guba Zoltán, Háder Márk István, Jánosik Áron, Kolontári Péter, Kondákor Márk, Kozák András, Lipták Gergő, Magyar Róbert Attila, Marozsák Tóbiás , Máth Benedek, Morvai Orsolya, Németh Csaba Tibor, Olosz Adél, Ónodi Gergely, Pszota Máté, Sal Dávid, Schneider Anna, Takács Árpád, Tófalusi Ádám, Viczián Anna. 4 points: Balogh Tamás, Bartók Imre, Berke Martin, Bonifert Balázs, Czett Mátyás, Édes Lili, Garamvölgyi István Attila, Jánosdeák Márk, Keltai Dóra, Klučka Vivien, Mamuzsics Gergő Bence, Markó Gábor, Molnár Mátyás, Pálfi Fanni, Póta Balázs, Rusvai Miklós, Shirsha Bose, Surján Botond, Tafferner Zoltán, Turcsányi Máté, Zirci Márton. 3 points: 4 students. 2 points: 3 students. 1 point: 3 students. 0 point: 2 students.
Problems in Physics of KöMaL, December 2017
