 |
A P. 4994. feladat (2018. január) |
P. 4994. Az ábrán látható ék és a rajta lévő tömör, \(\displaystyle R\) sugarú henger tömege egyaránt \(\displaystyle m\). Az ék a talajon súrlódás nélkül csúszhat. Legalább mekkora a tapadási súrlódási együttható értéke az ék és a henger között, ha a henger tisztán gördül, és az ék hajlásszöge \(\displaystyle \alpha=30^\circ\)?
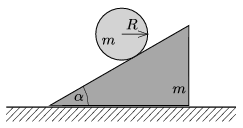
Közli: Berke Martin, Zalaegerszeg, Zrínyi M. Gimn.
(5 pont)
A beküldési határidő 2018. február 12-én LEJÁRT.
Megoldás. Jelöljük az ék vízszintes gyorsulását (jobbra) \(\displaystyle A\)-val, a henger gyorsulását az ékhez viszonyítva \(\displaystyle a\)-val, a henger szöggyorsulását \(\displaystyle \beta\)-val, a tapadó súrlódási erőt \(\displaystyle S\)-sel, végül a henger és az ék közötti nyomóerőt \(\displaystyle N\)-nel (lásd az ábrát).
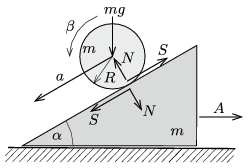
A következő mozgásegyenleteket írhatjuk fel:
\(\displaystyle SR=\frac{1}{2}mR^2\beta,\)
\(\displaystyle N\sin\alpha-S\cos\alpha=mA,\)
\(\displaystyle mg-S\sin\alpha-N\cos\alpha=ma\sin\alpha,\)
\(\displaystyle N\sin\alpha-S\cos\alpha=m(a\cos\alpha-A),\)
továbbá a tiszta (csúszásmentes) gördülés feltételét:
\(\displaystyle a-R\beta=0.\)
Ezekből az egyenletekből következik, hogy
\(\displaystyle A=\frac{\cos\alpha \,\sin\alpha}{3\sin^2\alpha+2\cos^2\alpha}g=\frac{g}{\sqrt{27}}=1{,}89~\frac{\rm m}{\rm s^2},\)
\(\displaystyle a=\frac{2\sin\alpha}{3\sin^2\alpha+2\cos^2\alpha}g=\frac{4g}{9}=4{,}36~\frac{\rm m}{\rm s^2},\)
\(\displaystyle S=\frac{\sin\alpha}{3\sin^2\alpha+2\cos^2\alpha}mg=\frac{2}{9}mg,\)
\(\displaystyle N=\frac{2\cos\alpha}{3\sin^2\alpha+2\cos^2\alpha}mg=\frac{4}{\sqrt{27}}mg.\)
A csúszásmentes gördülés feltétele:
\(\displaystyle \mu\ge \frac{S}{N}= \frac{1}{2}\tg\alpha=\frac{1}{\sqrt{12}}\approx 0{,}29.\)
Statisztika:
45 dolgozat érkezett. 5 pontot kapott: Bartók Imre, Berke Martin, Elek Péter, Fajszi Bulcsú, Fekete Balázs Attila, Illés Gergely, Jánosik Áron, Kolontári Péter, Kondákor Márk, Marozsák Tóbiás , Máth Benedek, Olosz Adél, Richlik Róbert, Sal Dávid. 4 pontot kapott: Csuha Boglárka, Lipták Gergő, Markó Gábor, Póta Balázs. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 13 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2018. januári fizika feladatai

