Problem P. 4994. (January 2018)

P. 4994. The masses of both the wedge and the solid cylinder shown in the figure are \(\displaystyle m\), the radius of the cylinder is \(\displaystyle R\). The wedge can slide without friction on the ground. What is the minimum value of the coefficient of static friction between the wedge and the cylinder, if the cylinder rolls without slipping along the wedge and the angle of elevation of the wedge is \(\displaystyle \alpha=30^\circ\)?

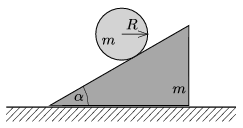
(5 pont)

Deadline expired on February 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük az ék vízszintes gyorsulását (jobbra) \(\displaystyle A\)-val, a henger gyorsulását az ékhez viszonyítva \(\displaystyle a\)-val, a henger szöggyorsulását \(\displaystyle \beta\)-val, a tapadó súrlódási erőt \(\displaystyle S\)-sel, végül a henger és az ék közötti nyomóerőt \(\displaystyle N\)-nel (lásd az ábrát).

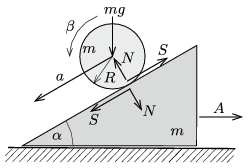
A következő mozgásegyenleteket írhatjuk fel:

\(\displaystyle SR=\frac{1}{2}mR^2\beta,\)

\(\displaystyle N\sin\alpha-S\cos\alpha=mA,\)

\(\displaystyle mg-S\sin\alpha-N\cos\alpha=ma\sin\alpha,\)

\(\displaystyle N\sin\alpha-S\cos\alpha=m(a\cos\alpha-A),\)

továbbá a tiszta (csúszásmentes) gördülés feltételét:

\(\displaystyle a-R\beta=0.\)

Ezekből az egyenletekből következik, hogy

\(\displaystyle A=\frac{\cos\alpha \,\sin\alpha}{3\sin^2\alpha+2\cos^2\alpha}g=\frac{g}{\sqrt{27}}=1{,}89~\frac{\rm m}{\rm s^2},\)

\(\displaystyle a=\frac{2\sin\alpha}{3\sin^2\alpha+2\cos^2\alpha}g=\frac{4g}{9}=4{,}36~\frac{\rm m}{\rm s^2},\)

\(\displaystyle S=\frac{\sin\alpha}{3\sin^2\alpha+2\cos^2\alpha}mg=\frac{2}{9}mg,\)

\(\displaystyle N=\frac{2\cos\alpha}{3\sin^2\alpha+2\cos^2\alpha}mg=\frac{4}{\sqrt{27}}mg.\)

A csúszásmentes gördülés feltétele:

\(\displaystyle \mu\ge \frac{S}{N}= \frac{1}{2}\tg\alpha=\frac{1}{\sqrt{12}}\approx 0{,}29.\)

Statistics:

45 students sent a solution.
5 points:	Bartók Imre, Berke Martin, Elek Péter, Fajszi Bulcsú, Fekete Balázs Attila, Illés Gergely, Jánosik Áron, Kolontári Péter, Kondákor Márk, Marozsák Tóbiás , Máth Benedek, Olosz Adél, Richlik Róbert, Sal Dávid.
4 points:	Csuha Boglárka, Lipták Gergő, Markó Gábor, Póta Balázs.
3 points:	7 students.
2 points:	13 students.
1 point:	1 student.
0 point:	4 students.
Unfair, not evaluated:	2 solutionss.

Problems in Physics of KöMaL, January 2018