 Problem P. 4997. (January 2018)
Problem P. 4997. (January 2018)
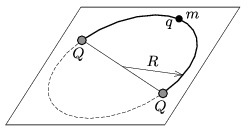
P. 4997. A point-like bead of mass \(\displaystyle m\), and of charge \(\displaystyle q\) can move frictionlessly along a horizontal semicircular path of radius \(\displaystyle R\). At each end of the semicircle there is a point-like fixed object of charge \(\displaystyle Q\). The system described is in equilibrium. What is the period of the motion of the bead if it is displaced a bit from its equilibrium position and then released?
(5 pont)
Deadline expired on February 12, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A gyöngy a félkörív felezőpontjában, a rögzített ponttöltésektől egyenlő távolságban lehet egyensúlyban. Térítsük ki a gyöngyöt ebből az egyensúlyi helyzetből egy kicsiny, a félkörív mentén mért \(\displaystyle s\) elmozdulással (\(\displaystyle s\ll R\)), és jelöljük a félkörív középpontjához húzott sugár szögének elfordulását \(\displaystyle 2\varphi\)-vel (\(\displaystyle \varphi\ll 1)\). Az elmozdulás és a szögelfordulás közötti kapcsolat: \(\displaystyle s=2R\varphi\).
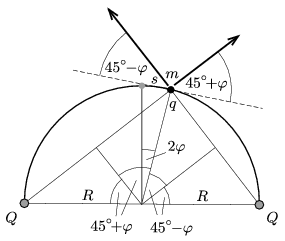
Számítsuk ki a kicsit kimozdított gyöngyre ható eredő erő érintő irányú komponensét! A Coulomb-törvény szerint (az ábrán jelölt távolságok és szögek ismeretében)
\(\displaystyle F(s)=k\frac{qQ}{4R^2}\left[ \frac{\cos(45^\circ+\varphi)}{\sin^2(45^\circ+\varphi)}-\frac{\cos(45^\circ-\varphi)}{\sin^2(45^\circ-\varphi)} \right].\)
A szögletes zárójelben álló kifejezés az addíciós tételek szerint így írható:
\(\displaystyle [\ldots]=-\sqrt{2}\frac{6\cos^2\varphi\sin\varphi+2\sin^3\varphi}{\left(\cos^2\varphi-\sin^2\varphi\right)^2},\)
ami \(\displaystyle \varphi\ll 1\) miatt (\(\displaystyle \cos\varphi\approx 1\) és \(\displaystyle \sin\varphi\approx \varphi\) közelítésekkel, valamint a \(\displaystyle \varphi\) szög 1-nél magasabb kitevőjű hatványainak elhanyagolásával) a következő egyszerű alakot ölti:
\(\displaystyle [\ldots]\approx -6\sqrt{2}\, \varphi.\)
A gyöngyszemet visszahúzó eredő erő tehát
\(\displaystyle F(s)=-D\,s,\qquad \text{ahol} \qquad D= \frac{3kqQ}{\sqrt{8}R^3}.\)
Ez megegyezik egy \(\displaystyle D\) direkciós erejű rugó által kifejtett erővel, a gyöngyszem mozgása tehát harmonikus rezgőmozgás lesz
\(\displaystyle T=2\pi \sqrt{\frac{\sqrt{8}mR^3}{3kqQ}}\)
periódusidővel.
Statistics:
21 students sent a solution. 5 points: Elek Péter, Kozák András, Marozsák Tóbiás , Olosz Adél, Takács Árpád. 4 points: Fajszi Bulcsú, Fekete Balázs Attila, Jánosik Áron, Magyar Róbert Attila, Máth Benedek, Molnár Mátyás, Póta Balázs, Sal Dávid, Surján Botond. 3 points: 6 students. 2 points: 1 student.
Problems in Physics of KöMaL, January 2018
