 Problem P. 4998. (January 2018)
Problem P. 4998. (January 2018)
P. 4998. A ray of light enters into a spherical water droplet, and after three total internal reflections it travels into its original direction as shown in the figure. What was the angle of incidence of the ray when it entered into the droplet? (The refractive index of water is \(\displaystyle n=4/3\).)
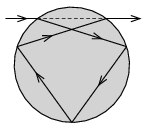
(5 pont)
Deadline expired on February 12, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha a vízsugár beesési szöge \(\displaystyle \alpha\), törési szöge \(\displaystyle \beta\), akkor fennáll: \(\displaystyle \sin\beta=\tfrac34 \sin\alpha\). A fénysugár irányváltozása (az óramutató járásával megegyező irányban) az első törésnél \(\displaystyle \alpha-\beta\), mindegyik belső visszaverődésnél \(\displaystyle 180^\circ-2\beta\), és a vízcseppből való kilépésnél ismét \(\displaystyle \alpha-\beta\). A megadott feltétel szerint a fénysugár egyszer ,,körbefordul'', tehát
\(\displaystyle (\alpha-\beta)+3(180^\circ-2\beta)+(\alpha-\beta)=360^\circ,\)
vagyis
\(\displaystyle 4\beta=\alpha+90^\circ,\)
így
\(\displaystyle \cos(4\beta)=\cos(\alpha+90^\circ)=-\sin\alpha=-\frac43\sin\beta.\)
(Az utolsó lépésnél felhasználtuk a törési törvényt.)
A \(\displaystyle \cos(4\beta)+ \tfrac43\sin\beta=0\) trigonometrikus egyenletet akár egy zsebszámológéppel, próbálgatással is megoldhatjuk. (Figyelembe kell vegyük, hogy \(\displaystyle \sin\beta\le \frac{1}{n}=\frac{3}{4}\), vagyis \(\displaystyle \beta\) legfeljebb \(\displaystyle 48{,}6^\circ\) lehet.) Az eredmény: \(\displaystyle \beta=34{,}9^\circ\), és ennek megfelelően a fénysugár belépési szöge: \(\displaystyle \alpha=49{,}8^\circ\).
Megjegyzés. Ha a háromszor visszaverődő és kétszer megtörő fénysugár irányváltozására nem \(\displaystyle 360^\circ\)-ot, hanem valamekkora más \(\displaystyle \varphi\) szöget írunk elő, akkor bizonyos \(\displaystyle \varphi\) szögekre a feladatnak nincs megoldása. A határeset \(\displaystyle \varphi_0=41{,}4^\circ\), ez a harmadrendű szivárvány látószöge felének felel meg.
Statistics:
42 students sent a solution. 5 points: Bartók Imre, Beke Csongor, Bíró Dániel, Bonifert Balázs, Bukor Benedek, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Édes Lili, Elek Péter, Fajszi Bulcsú, Fekete András Albert, Fekete Balázs Attila, Jánosik Áron, Kolontári Péter, Kondákor Márk, Magyar Róbert Attila, Makovsky Mihály, Mamuzsics Gergő Bence, Markó Gábor, Marozsák Tóbiás , Olosz Adél, Póta Balázs, Rusvai Miklós, Sal Dávid, Sas 202 Mór, Schrott Márton, Surján Botond, Tafferner Zoltán. 4 points: Balaskó Dominik, Békési Ábel, Geretovszky Anna, Kozák András, Szakály Marcell. 3 points: 5 students. 2 points: 1 student. 1 point: 2 students.
Problems in Physics of KöMaL, January 2018
