 |
A P. 5000. feladat (2018. január) |
P. 5000. Az ábrán látható U-alakú csőbe vizet töltöttünk. Hogyan és mennyire változik meg a cső két szárában a víz szintje, ha a bal oldali csőszárat szorosan körülvevő \(\displaystyle N\) menetes, \(\displaystyle \ell\) hosszúságú tekercsbe \(\displaystyle I\) erősségű áramot vezetünk? (A cső átmérője jóval kisebb a tekercs hosszánál. A víz relatív permeabilitása \(\displaystyle \mu_{\rm r}\), számértéke 1-nél egy nagyon kicsivel kisebb.)
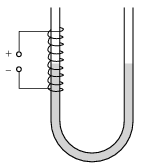
(Lásd még Radnai Gyula: Az elektromágnes húzóerejéről szóló cikket a KöMaL 2000. évi 4. számában és a honlapunkon.)
Közli: Vigh Máté, Budapest
(6 pont)
A beküldési határidő 2018. február 12-én LEJÁRT.
I. megoldás. Jelöljük a tekercsben lévő vízoszlop magasságát az áram bekapcsolása előtt \(\displaystyle x_0\)-lal. Az áram bekapcsolása miatt változzon meg ez a magasság \(\displaystyle x\)-szel, vagyis legyen a vízszintek magasságkülönbsége \(\displaystyle 2x\), és a tekercset \(\displaystyle x_0+x\) magasan töltse ki a víz. Ebben a helyzetben az \(\displaystyle A\) keresztmetszetű, \(\displaystyle \ell\) hosszúságú, \(\displaystyle N\) menetes tekercs önindukciós együtthatója (ami a gerjesztési törvényből kapható meg, de a hivatkozott cikkben is megtalálható):
| \(\displaystyle (1)\) | \(\displaystyle L(x)=\mu_0\frac{N^2A}{\ell}\bar{\mu}(x), \) |
ahol a tekercsben lévő anyag átlagos relatív permeabilitását így számolhatjuk ki:
| \(\displaystyle (2)\) | \(\displaystyle \frac{1}{\bar{\mu}(x)}=\frac{x_0+x}{\ell}\frac{1}{\mu_{\rm r}}+\frac{\ell-x_0-x}{\ell}. \) |
Megjegyzés. A fenti képlet a gerjesztési törvény közegben is érvényes alakjából kapható meg:
\(\displaystyle \sum_\text{zárt görbére}\frac{1}{\mu_{\rm r}({\boldsymbol r})}{\boldsymbol B({\boldsymbol r})}\,\Delta {\boldsymbol r}=\mu_0 \sum_\text{körülvett felületre} I.\)
Esetünkben, amikor a tekercsen kívül elhanyagolható a mágneses indukció, a belsejében pedig \(\displaystyle B\) állandó, a gerjesztési törvény így írható fel:
\(\displaystyle \frac{B\cdot(x_0+x)}{\mu_{\rm r}}+B\cdot(\ell-x_0-x)=NI,\)
az \(\displaystyle N\) meneten áthaladó összes fluxus tehát
\(\displaystyle \Phi=LI=BAN=\frac{\mu_0 N^2AI}{ \frac{x_0+x}{\mu_{\rm r}}+ (\ell-x_0-x) }.\)
Vizsgáljuk meg, mekkora energiával rendelkezik az áramjárta tekercs és a csőben lévő víz együttesen, amikor a vízfelszín \(\displaystyle x\)-szel elmozdult az árammentes esethez képest. A tekercs energiája ebben az állapotban \(\displaystyle \tfrac12 LI^2,\) a víz helyzeti energiája pedig (az eredeti helyzethez viszonyítva) \(\displaystyle \varrho gA x^2\).
Mi történne, ha a vízszint – valamilyen ok miatt – egy kicsiny \(\displaystyle \Delta x\) értékkel megemelkedne? A víz helyzeti energiája ekkor
\(\displaystyle \Delta E_\text{helyzeti}=2\varrho g A x \Delta x\)
értékkel megnőne, hiszen a megváltozott állapotot úgy is megkaphatjuk, hogy a jobb oldali csőszárból egy \(\displaystyle \varrho A\Delta x\) tömegű kis vizhengert a bal oldali \(\displaystyle 2x\)-szel magasabban lévő tetejére helyezünk. A tekercs mágneses energiája is megváltozik, hiszen \(\displaystyle L\) függ a vízmagasságtól. Állandó áramerősség mellett (és kihasználva, hogy \(\displaystyle \mu_{\rm r}\approx 1\)) az (1) és (2) képletek alapján
\(\displaystyle \Delta E_\text{mágneses}=\Delta \left(\frac12 LI^2\right)=\frac{I^2}{2}\Delta L\approx -\mu_0\frac{N^2AI^2}{2\ell^2}(1-\mu_{\rm r})\Delta x. \)
Nem szabad megfeledkeznünk arról, hogy a tekercs és a csőben lévő víz energetikailag nem alkot zárt rendszert, hiszen a tekercs össze van kötve az áramforrással. Amikor a tekercs önindukciós együtthatója (\(\displaystyle x\) változása miatt) egy kicsit megváltozik, a tekercs fluxusa is megváltozik
\(\displaystyle \Delta\Phi=I\Delta L\)
értékkel, és ez a változás (ha \(\displaystyle \Delta t\) idő alatt következik be) Faraday-törvénye szerint
\(\displaystyle U=\frac{\Delta\Phi}{\Delta t}\)
nagyságú feszültséget indukál a tekercsben. Ez a feszültség csökkenteni igyekszik \(\displaystyle \Phi\) változását (Lenz-törvény). Ha az áramforrás fenn akarja tartani az állandó \(\displaystyle I\) áramerősséget,
\(\displaystyle W=UI\Delta t=I\Delta\Phi=I^2\Delta L\)
többletenergiát kell leadjon (az eredeti, a Joule-hő fedezésére szolgáló energialeadáson felül).
Egyensúlyi állapotban teljesül, hogy
\(\displaystyle W=\Delta E_\text{mágneses}+\Delta E_\text{helyzeti},\)
vagyis
\(\displaystyle I^2\Delta L=\frac12 I^2\Delta L+2\varrho g A x \Delta x.\)
(Ha \(\displaystyle W\) nagyobb vagy kisebb lenne, mint a mágneses és a gravitációs energia változásának összege, akkor – valamilyen előjelű \(\displaystyle \Delta x\) mellett – még mozgási energiára is szert tehetne a víz, tehát nem maradna egyensúlyban.)
A fenti egyenletből következik, hogy
\(\displaystyle x=\frac{I^2}{4\varrho g A}\frac{\Delta L}{\Delta x}=-\frac{\mu_0(1-\mu_{\rm r})N^2I^2}{4\ell^2\varrho g}<0.\)
A víz szintje tehát a bal oldali szárban lesüllyed.
II. megoldás. A vízoszlop egyensúlyi állapotában a mágneses és a gravitációs erők egyensúlyban vannak. A mágneses erők nagyságát egyértelműen meghatározza a tekercsben folyó áram, és az erő nem függ attól, hogy mekkora a vezeték ellenállása. Lehetne ez a vezeték akár szupravezető (nulla elektromos ellenállású) is, a vízoszlop egyensúlyi magasságát ez a lehetőség nem változtatná meg.
Egy szupravezető tekercsben akkor is fennmarad az áram, ha nem kapcsolunk rá külső áramforrást. Ilyen körülmények között a tekercs és az U-alakú csőben lévő víz energetikailag zárt rendszert alkot, a helyzeti energiája az egyensúlyi állapotban minimális. (A rendszer helyzeti energiája a mechanikai mozgástól független energiafajtáit jelenti; a mágneses tér energiája is ilyen jellegű.)
Az I. megoldás gondolatmenetét követve állíthatjuk:
\(\displaystyle E_\text{összes}= E_\text{mágneses}+ E_\text{helyzeti}=\frac{1}{2}LI^2+\varrho g A x^2=\text{minimum},\)
vagyis kicsiny \(\displaystyle \Delta x\) vízszintváltozásra
\(\displaystyle \Delta E_\text{mágneses}+\Delta E_\text{helyzeti}=0.\)
Nem szabad elfelejtenünk, hogy egy szupravezető tekercsben a \(\displaystyle \Phi=LI\) fluxus nem változhat meg (hiszen tetszőlegesen kicsiny fluxusváltozás feszültséget indukálna, ami a nulla ellenállás miatt ,,végtelen nagy'' áramot hozna létre). Ha tehát egy ilyen tekercsben valamilyen ok miatt \(\displaystyle L(x)\) változik, az áramerősség sem maradhat állandó.
Fejezzük ki a rendszer energiáját az áramerősség helyett a mágneses fluxussal:
\(\displaystyle E_\text{összes}=\frac{\Phi^2}{2L(x)}+\varrho g A x^2 =\text{minimum},\)
vagyis
\(\displaystyle \frac{\Phi^2}{2}\,\Delta\left(\frac1{L(x)} \right)+\varrho g A \Delta\left( x^2 \right)=0.\)
Felhasználva, hogy
\(\displaystyle \Delta\left(\frac1{L(x)} \right)=\frac{1}{L+\Delta L}-\frac{1}{L}\approx -\frac{\Delta L}{L^2}, \qquad \text{illetve}\qquad \Delta\left( x^2 \right)=(x+\Delta x)^2-x^2\approx 2x \Delta x,\)
a vízszintváltozásra kapjuk:
\(\displaystyle x=\frac{\Phi^2}{4L^2\varrho g A}\,\frac{\Delta L}{\Delta x}\approx -\frac{\mu_0(1-\mu_{\rm r})N^2I^2}{4\ell^2\varrho g}<0.\)
(Az utolsó lépésben kihasználtuk, hogy \(\displaystyle \Phi=LI\), és behelyettesítettük \(\displaystyle L(x)\)-nek az I. megoldásban szereplő konkrét alakját.)
III. megoldás. Ismert, hogy a mágneses mező energiasűrűsége (egységnyi térfogatban lévő energia) vákuumban \(\displaystyle B^2/(2\mu_0),\) mágnesesen polarizálható közegben pedig
\(\displaystyle \frac{\text{energia}}{\text{térfogat}}=\frac{B^2}{2\mu_0\mu_{\rm r}},\)
ahol \(\displaystyle \mu_{\rm r}\) a közeg relatív permeabilitása. Ebből következik, hogy a mágneses mező a közeg egységnyi felületére
\(\displaystyle \sigma=\frac{B^2}{2\mu_0\mu_{\rm r}}\)
húzóerőt (negatív nyomást) fejt ki.
Megjegyzés. a fenti képletet úgy láthatjuk be, hogy elképzelünk egy téglatest alakú térrészt, amelynek egyik, \(\displaystyle A\) területű oldallapját \(\displaystyle F\) erő kifejtésével kicsiny \(\displaystyle \Delta x\)-szel kifelé húzzuk. Az eközben végzett munka \(\displaystyle F\Delta x\), a térrész mágneses energiájának növekedése pedig az energiasűrűség és \(\displaystyle A\Delta x\) szorzata. A munkatétel szerint
\(\displaystyle F\Delta x=\frac{B^2}{2\mu_0\mu_{\rm r}}A\Delta x,\)
ahonnan a \(\displaystyle \sigma=F/A\) húzófeszültségre a fentebb megadott összefüggés adódik.
Ha az U-alakú csőben \(\displaystyle 2x\) szintkülönbség alakul ki, a hidrosztatikai nyomással a mágneses húzófeszültségek különbsége tart egyensúlyt.
\(\displaystyle 2\varrho g x=\frac{B^2}{2\mu_0\mu_{\rm r}}-\frac{B^2}{2 \mu_{\rm r}},\)
ahonnan
\(\displaystyle x=\frac{B^2}{4\mu_0\varrho g}\left(\frac{1}{\mu_0}-1\right)\approx \frac{\mu_0(1-\mu_{\rm r})N^2I^2}{4\ell^2\varrho g}.\)
(Az utolsó lépésben kihasználtuk, hogy \(\displaystyle \mu_{\rm r}\) csak nagyon kicsit tér el 1-től, emiatt a tekercs belsejében \(\displaystyle B\) lényegében ugyanakkora, mint vákuumban lenne.
A víz (diamágneses anyag) relatív permeabilitása 1-nél kisebb, így a mágneses mező húzófeszültsége a vízfelület alsó oldalán nagyobb, mint a felső (levegő felöli) oldalon; a víz tehát a bal oldali szárban lesüllyed.
Statisztika:
11 dolgozat érkezett. 6 pontot kapott: Elek Péter, Olosz Adél. 5 pontot kapott: Fajszi Bulcsú, Fekete Balázs Attila, Kondákor Márk, Marozsák Tóbiás , Sal Dávid. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2018. januári fizika feladatai

