 Problem P. 5013. (March 2018)
Problem P. 5013. (March 2018)
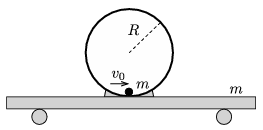
P. 5013. The total mass of the trolley, which has small light wheels, and the ring of radius \(\displaystyle R=1\) m on the trolley is \(\displaystyle m\) (see the figure). A small point-like object of mass \(\displaystyle m\) is placed to the bottom of the ring. The small object is given an initial speed of \(\displaystyle v_0\). What is the value of \(\displaystyle v_0\) if the trolley just rises from the ground when the object reaches the topmost point of the ring? Friction is negligible everywhere.
(5 pont)
Deadline expired on April 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Legyen a test sebessége a pályájának legmagasabb pontjában \(\displaystyle v_1\), a kocsi sebessége ugyanekkor \(\displaystyle v_2\). Az energia- és a lendületmegmaradás törvénye szerint
\(\displaystyle mv_0=mv_1+ mv_2,\qquad \text{illetve}\qquad \frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2+\frac{1}{2}mv_2^2+2mgR.\)
Az egyenletrendszer (\(\displaystyle v_1<v_2\) feltételnek eleget tevő) megoldása
\(\displaystyle v_1=\frac{v_0}{2}-\sqrt{\left(\frac{v_0}{2}\right)^2-2gR},\qquad v_2=\frac{v_0}{2}+\sqrt{\left(\frac{v_0}{2}\right)^2-2gR}.\)
Számítsuk most ki a pontszerű testre ható \(\displaystyle K\) erő nagyságát a pálya legmagasabb pontjában! Ha ez nagyobb, mint \(\displaystyle mg\), akkor a kiskocsi \(\displaystyle K\) ellenereje hatására megemelkedik. (Belátható, hogy a megemelkedés szempontjából a pálya legfelső pontja a kritikus, ha ott nem teljesül a \(\displaystyle K>mg\) feltétel, akkor máshol sem emelkedhet fel a kiskocsi.)
Írjuk fel a kis test mozgásegyenletét a pálya legfelső pontjában a kocsihoz rögzített koordináta-rendszerben. Ez a rendszer ugyan nem inerciarendszer, de mivel a kérdéses pillanatban a kocsi gyorsulása nulla, a Newton-egyenlet eredeti alakjában érvényes. A kis test ebben a rendszerben \(\displaystyle R\) sugarú körpályán mozog, sebessége a legfelső pontban \(\displaystyle v_1-v_2\), a mozgásegyenlet tehát
\(\displaystyle mg+K=m\frac{\left(v_2-v_1\right)^2}{R},\)
vagyis
\(\displaystyle K=\frac{mv_0^2}{R}-9mg>mg,\qquad \text{azaz}\qquad v_0>\sqrt{10\,gR}\approx 10~\frac{ \rm m}{\rm s}.\)
II. megoldás. A feladatot megoldhatjuk inerciarendszerből, például a tömegközépponthoz rögzített vonatkoztatási rendszerből is. Ebben a rendszerben a pontszerű test kezdősebessége \(\displaystyle v_0/2\) jobbra, a kiskocsi pedig ugyanekkora sebességgel mozog balra az indulás pillanatában. Ha a kiskocsi vízszintes elmozdulása egy adott pillanatban \(\displaystyle x\), akkor a kocsié ugyanekkora nagyságú, de ellentétes irányú lesz. Amennyiben a kis test függőleges elmozdulása \(\displaystyle y\), akkor a gyűrűn maradás kényszerfeltétele:
\(\displaystyle (x+x)^2+(y-R)^2=R^2.\)
Ez egy \(\displaystyle a=R\) nagytengelyű, \(\displaystyle b=R/2\) kistengelyű ellipszis egyenlete. Az ellipszis görbületi sugara a nagytengely végpontjaiban, így a pálya legmagasabb pontjában is
\(\displaystyle r=\frac{b^2}{a}=\frac{R}{4}.\)
A kis test \(\displaystyle u\) sebessége a pálya legfelső pontjában az energiamegmaradás törvényéből számolható:
\(\displaystyle 2\cdot \frac{m}{2}\left(\frac{v_0}{2}\right)^2=2\cdot\frac{mu^2}{2}+2mgR,\)
ahonnan
\(\displaystyle u^2=\frac{v_0^2}{4}-2gR.\)
A test mozgásegyenlete a pálya legfelső pontjában
\(\displaystyle mg+K=m\frac{u^2}{r}, \qquad \text{ahonnan}\qquad K=\frac{mu^2}{(R/4)}-mg=\frac{mv_0^2}{R}-9\,mg.\)
Innen \(\displaystyle K>mg\) miatt \(\displaystyle v_0>\sqrt{10\,gR}.\)
Statistics:
48 students sent a solution. 5 points: Bartók Imre, Békési Ábel, Berke Martin, Bíró Dániel, Csire Roland, Csuha Boglárka, Elek Péter, Fajszi Bulcsú, Fekete Balázs Attila, Fialovszky Márk, Guba Zoltán, Illés Gergely, Jánosik Áron, Kondákor Márk, Kozák András, Magyar Róbert Attila, Makovsky Mihály, Mamuzsics Gergő Bence, Marozsák Tóbiás , Máth Benedek, Molnár Mátyás, Olosz Adél, Ónodi Gergely, Pácsonyi Péter, Pálfi Fanni, Póta Balázs, Sal Dávid, Sas 202 Mór, Surján Botond, Turcsányi Ádám, Viczián Anna. 4 points: Kovács Gergely Balázs, Markó Gábor, Németh Csaba Tibor, Tafferner Zoltán, Zeke Norbert. 3 points: 10 students. 2 points: 2 students.
Problems in Physics of KöMaL, March 2018
