 Problem P. 5026. (April 2018)
Problem P. 5026. (April 2018)
P. 5026. A thin ring of mass \(\displaystyle m\) and of radius \(\displaystyle R\) is made swing with small amplitude in two different ways. In one of the cases the ring is supported by a horizontal cylinder of radius \(\displaystyle r\), displaced a bit and then released. In the other case a thin pin of length \(\displaystyle r\) and of negligible mass is attached to the inside part of the ring, such that it points towards the centre of the ring, and the ring is supported by this pin while it swings. The motion of the ring is planar in both cases.
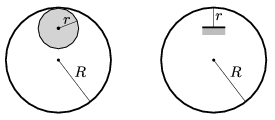
In which case will the period of the oscillation be larger?
(5 pont)
Deadline expired on May 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A tű hegye körül elforduló gyűrű egy fizikai inga, amelynek lengésideje (kis kitérések esetén)
\(\displaystyle T_1=2\pi\sqrt{\frac{ mR^2+m(R-r)^2}{mg(R-r)}}=2\pi\sqrt{\frac{ 2R^2+r^2-2rR}{ g(R-r)}}.\)
A hengeren csúszásmentesen gördülő gyűrű mozgása bonyolultabb, hiszen a pillanatnyi forgástengely (a karika és a henger \(\displaystyle A\) érintkezési pontja) pillanatról pillanatra változó helyen található. Jelöljük a gyűrű \(\displaystyle A\) körüli szögsebességét \(\displaystyle \Omega_A\)-val! A gyűrű mozgási energiája ekkor
\(\displaystyle E_\text{mozgási}=\frac{1}{2}I_A\Omega_A^2,\)
ahol a Steiner-tétel szerint \(\displaystyle I_A=2mR^2\).
Fejezzük ki a mozgási energiát a henger (időben állandó helyzetű) \(\displaystyle P\) ,,középpontja'' körüli elfordulás \(\displaystyle \Omega_P\) szögsebessége segítségével! Mivel a gyűrű \(\displaystyle K\) középpontjának sebessége kétféle módon is felírható:
\(\displaystyle v_K=R\Omega_A=(R-r)\Omega_P,\)
tehát
\(\displaystyle \Omega_A=\frac{R-r}{R}\Omega_P,\)
és így a mozgási energia
\(\displaystyle E_\text{mozgási}=m(R-r)^2\Omega_P^2.\)
Ha az \(\displaystyle AK\) egyenes \(\displaystyle \varphi\) szöget zár be a függőlegessel, akkor a karika gravitációs helyzeti energiája
\(\displaystyle E_\text{helyzeti}=mg(R-r)(1-\cos\varphi)=mg(R-r)\cdot 2\sin^2\frac{\varphi}{2}\approx mg(R-r)\frac{\varphi^2}{2}.\)
Tudjuk továbbá, hogy
\(\displaystyle \Omega_P=\frac{\Delta\varphi}{\Delta t},\)
vagyis \(\displaystyle \Omega_P\) az időben változó \(\displaystyle \varphi(t)\) változási sebessége (deriváltja).
A harmonikus rezgőmozgás képleteit használva felírhatjuk:
\(\displaystyle \varphi(t)=\varphi_\text{max} \sin\omega t,\)
\(\displaystyle \Omega_P(t)=\varphi_\text{max} \omega \cos\omega t,\)
ahol \(\displaystyle \omega=2\pi/T\) (\(\displaystyle T\) a rezgés periódusideje).
Ezek ismeretében megadhatjuk a helyzeti és a mozgási energia időbeli változásának képleteit:
\(\displaystyle E_\text{helyzeti}(t)= \frac{1}{2}mg(R-r) \varphi_\text{max}^2\sin^2(\omega t), \)
\(\displaystyle E_\text{mozgási}(t)= m(R-r)^2\omega^2 \varphi_\text{max}^2\cos^2(\omega t). \)
A gyűrű teljes energiája időben állandó mennyiség:
\(\displaystyle E=E_\text{helyzeti}(t)+E_\text{mozgási}(t)=\text{állandó}+\frac{1}{2}mg(R-r) \varphi_\text{max}^2\cos^2(\omega t)\left[\frac{2\omega^2(R-r)}{g}-1\right]. \)
Ez az energia akkor nem függ az időtől, ha a szögletes zárójelben álló kifejezés nulla, vagyis
\(\displaystyle \omega=\sqrt{\frac{g}{2(R-r)}},\)
és így a ,,gördüléses rezgőmozgás'' periódusideje
\(\displaystyle T_2=2\pi\frac{2(R-r)}{g}.\)
Megmutatjuk, hogy \(\displaystyle T_1>T_2\), tehát a tű csúcsán billegő gyűrű lengésideje nagyobb, mint a gördülő gyűrűé. Valóban (a fizikailag megvalósítható \(\displaystyle 0<r<R\) tartományban)
\(\displaystyle \left(\frac{T_1}{T_2}\right)^2=\frac{2R^2+r^2-2Rr}{2(R-r)^2 } = 1+\frac{r(2R-r)}{2(R-r)^2}>1. \)
Statistics:
22 students sent a solution. 5 points: Elek Péter, Marozsák Tóbiás , Olosz Adél, Sal Dávid. 2 points: 6 students. 1 point: 10 students. 0 point: 2 students.
Problems in Physics of KöMaL, April 2018
