Problem P. 5066. (October 2018)

P. 5066. In a transparent medium the optical refractive index is changing in the direction of the axis \(\displaystyle z\) of the coordinate system. Perpendicular to this, in the direction of the axis \(\displaystyle x\) a thin light ray travels, and entering into the medium it is deflected towards the positive region of the axis \(\displaystyle z\) along a parabolic path. The refractive index is \(\displaystyle n_0\) at \(\displaystyle z=0\) and \(\displaystyle \sqrt{2}n_0\) at \(\displaystyle z=h\). How does the refractive index depend on \(\displaystyle z\)?

(6 pont)

Deadline expired on November 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Osszuk fel a közeget a \(\displaystyle z\)-tengelyre merőleges, egymáshoz igen közeli, vékony sávokra, és egy-egy sávon belül tekintsük a törésmutatót állandó nagyságúnak. Ez a közelítés annál jobban hasonlít a valóságos (folytonosan változó \(\displaystyle n(z)\)-nek megfelelő) esethez, minél keskenyebbek a szóban forgó sávok.

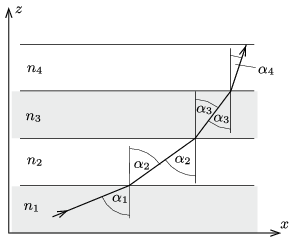
A vékony sávok határfelületénél felírhatjuk a Snellius–Descartes-féle törési törvényt:

\(\displaystyle \frac{n_1}{n_2}=\frac{\sin\alpha_1}{\sin\alpha_2}; \qquad \frac{n_2}{n_3}=\frac{\sin\alpha_2}{\sin\alpha_3}; \qquad \frac{n_3}{n_4}=\frac{\sin\alpha_3}{\sin\alpha_4} \ldots\)

vagyis

\(\displaystyle \frac{n_1}{\sin\alpha_1}=\frac{n_2}{\sin\alpha_2}=\frac{n_3}{\sin\alpha_3}=\ldots=\frac{n_k}{\sin\alpha_k}=\text{állandó}.\)

Itt \(\displaystyle n_i\) az \(\displaystyle i\)-edik réteghez tartozó törésmutató, \(\displaystyle \alpha_i\) pedig a fénysugár beesési szöge az \(\displaystyle i\)-edig réteg határán. Ezek szerint

\(\displaystyle n(z)=\text{állandó}\cdot \sin\alpha(z),\)

és mivel az \(\displaystyle x\) tengelynél \(\displaystyle n(0)=n_0\) és \(\displaystyle \alpha(0)=90^\circ\), felírhatjuk, hogy

\(\displaystyle n(z)=n_0\sin\alpha(z).\)

A feladat szövege szerint a fénysugár pályája parabolaív, amelynek egyenlete

\(\displaystyle z(x)=kx^2\)

alakban adható meg, ahol \(\displaystyle k\) egy (most még ismeretlen) állandó. A parabola ismert tulajdonsága, hogy az érintőjének meredeksége kétszer nagyobb, mint az adott pont és a parabola csúcspontja közötti szelő meredeksége. Ezt differenciálszámítással láthatjuk be, vagy egy ismert mechanikai analógiát felhasználva (az egyenletesen gyorsuló mozgás pillanatnyi sebességének és átlagsebességének összehasonlításából) kaphatjuk meg.

A fenti egyenlettel megadott parabola meredeksége tehát

\(\displaystyle \tg(90^\circ-\alpha)=\ctg\alpha=\frac{kx^2}{2x}=2kx=2\sqrt{kz}.\)

Másrészt

\(\displaystyle \sin\alpha=\frac{1}{1+\ctg^2\alpha},\)

tehát

\(\displaystyle n(z)\cdot \frac{1}{1+\ctg^2\alpha}=n_0, \qquad n(z)=n_0 \sqrt{1+4kz}.\)

Ha \(\displaystyle z=h\), akkor \(\displaystyle n=\sqrt{2}n_0,\) ahonnan

\(\displaystyle n_0 \sqrt{1+4kh}=\sqrt{2}n_0,\qquad 1+4kh=2,\qquad k=\frac{1}{4h}.\)

A keresett összefüggés tehát

\(\displaystyle n(z)=n_0\sqrt{1+\frac{z}{h}}.\)

Statistics:

14 students sent a solution.
6 points:	Bokor Endre, Bukor Benedek, Csépányi István, Elek Péter, Gulácsi Máté, Hisham Mohammed Almalki, Markó Gábor, Máth Benedek, Olosz Adél, Sal Dávid, Takács Árpád, Tiefenbeck Flórián.
3 points:	2 students.

Problems in Physics of KöMaL, October 2018