 Problem P. 5068. (November 2018)
Problem P. 5068. (November 2018)
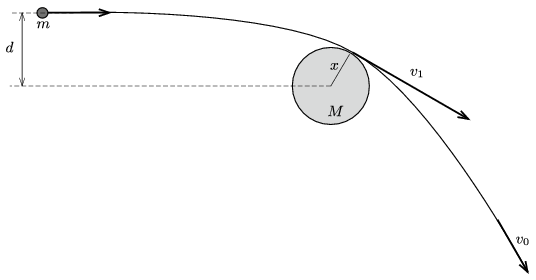
P. 5068. A small comet of mass \(\displaystyle m\), which can be considered point-like, approaches a spherical planet of mass \(\displaystyle M\), and of radius \(\displaystyle R\) (\(\displaystyle m\ll M\)). The speed of the comet very far from the planet is \(\displaystyle v_0\), and if the gravitational field of the planet did not exert any force on the comet, it would pass the planet at a distance of \(\displaystyle d\) from the centre of the planet (\(\displaystyle d>R\)). What is the minimum value of \(\displaystyle v_0\), at which the comet does not hit the planet? (Apart from the planet and the comet, the gravitational fields of any other celestial objects can be neglected.)
(5 pont)
Deadline expired on December 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük az üstökös maximális sebességét \(\displaystyle v_1\)-gyel, a bolygó középpontjától mért legkisebb távolságát pedig \(\displaystyle x\)-szel. A perdületmegmaradás törvénye szerint
\(\displaystyle mv_0d=mv_1x,\)
az energiamegmaradás törvénye pedig így alkalmazható:
\(\displaystyle \frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2-\gamma\frac{mM}{x}.\)
A fenti két egyenletből (\(\displaystyle v_1\) kiküszöbölése után)
\(\displaystyle x^2+2\frac{\gamma M}{v_0^2}x-d^2=0\)
adódik, amelynek (pozitív) megoldása:
\(\displaystyle x=\sqrt{ \left(\frac{\gamma M}{v_0^2}\right)^2+d^2}-\frac{\gamma M}{v_0^2}. \)
Az üstökös akkor nem ütközik a bolygóval, ha \(\displaystyle x>R\), vagyis
\(\displaystyle \sqrt{ \left(\frac{\gamma M}{v_0^2}\right)^2+d^2}-\frac{\gamma M}{v_0^2}>R,\)
azaz
\(\displaystyle \left(\frac{\gamma M}{v_0^2}\right)^2+d^2>\left(\frac{\gamma M}{v_0^2}+R\right)^2,\)
\(\displaystyle d^2-R^2>\frac{2\gamma M R}{v_0^2},\)
tehát
\(\displaystyle v_0>\sqrt{\frac{2\gamma MR}{d^2-R^2}} .\)
Statistics:
40 students sent a solution. 5 points: Békési Ábel, Bokor Endre, Bonifert Balázs, Csépányi István, Elek Péter, Forgács Kata, Fülöp Sámuel Sihombing, Kárpáti Kristóf, Kertész Balázs, Kozák 023 Áron, Lipták Gergő, Mácsai Dániel, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Merkl Gergely, Merkl Levente, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Sal Dávid, Simon Tamás, Székely Bálint, Szoboszlai Szilveszter, Tiefenbeck Flórián, Toronyi András, Turcsányi Máté, Varga Vázsony, Vaszary Tamás, Viczián Anna. 4 points: Bukor Benedek. 3 points: 2 students. 2 points: 1 student. 1 point: 1 student. 0 point: 5 students.
Problems in Physics of KöMaL, November 2018
