 Problem P. 5070. (November 2018)
Problem P. 5070. (November 2018)
P. 5070. There is a spring of spring constant \(\displaystyle D\) and of un-stretched length \(\displaystyle d\) in a cave of height \(\displaystyle \ell\). The spring is vertical, its mass is negligible and \(\displaystyle d<\ell\). One end of the spring is attached to the ceiling and the other is attached to the ground of the cave as shown in the figure.

A small bat of mass \(\displaystyle m\) flies to the midpoint of the spring, clings to the spring, and executes a complicated oscillatory motion driven by the spring. (Not any part of the spring gets loose during the motion of the bat.)
\(\displaystyle a)\) Where will the bat be when the oscillation is ceased? (The spring obeys Hooke's law even in the case of very big extensions.)
\(\displaystyle b)\) From this point the bat carefully climbs up to its original height of \(\displaystyle \ell/2\) measured from the ground. What is the least amount of work performed by the bat during its climb?
(5 pont)
Deadline expired on December 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük a megfeszített, de egyébként még terheletlen rugó egy olyan \(\displaystyle P\) pontját, amely a mennyezettől \(\displaystyle \ell_1\), a talajtól pedig \(\displaystyle \ell_2\) távolságban van (lásd az ábrát). Nyilván \(\displaystyle \ell_1+\ell_2=\ell\). Számítsuk ki, hogy mekkora \(\displaystyle x\) távolsággal süllyed le a rugó ezen pontja, ha ott \(\displaystyle F\) nagyságú, függőlegesen lefelé ható erőt fejtünk ki a rugóra.
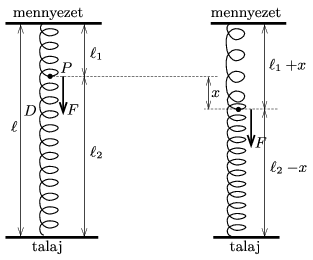
A rugó \(\displaystyle P\) feletti részének nyújtatlan hossza \(\displaystyle d_1\), az alsó rugódarabé pedig \(\displaystyle d_2\). Nyilván fennáll, hogy \(\displaystyle d_1+d_2=d\), és mivel az egyes rugórészekre és a teljes rugóra is ugyanakkora erő hat denevér nélkül:
\(\displaystyle \frac{d}{d_1}=\frac{\ell}{\ell_1},\qquad \frac{d}{d_2}=\frac{\ell}{\ell_2}.\)
A felső rugó megnyúlása
\(\displaystyle \ell_1+x-d_1=d_1\left(\frac\ell{d}-1\right)+x,\)
a benne ébredő erő tehát
\(\displaystyle F_1=D\frac{d}{d_1}d_1\left(\frac\ell{d}-1\right)+D\frac{d}{d_1}x=D(\ell-d)+D\frac{\ell}{\ell_1}x.\)
Felhasználtuk, hogy a rugó felső részének megfelelő rugódarab rugóállandója a hosszával fordítottan arányos, esetünkben tehát \(\displaystyle D_1=Dd/d_1=D\ell/\ell_1\), és hasonlóan az alsó rész rugóállandója \(\displaystyle D_2=D\ell/\ell_2\). Ennek megfelelően az alsó rugódarab által (függőlegesen lefelé) kifejtett erő:
\(\displaystyle F_2=D(\ell-d)-D\frac{\ell}{\ell_2}x,\)
vagyis a teljes külső erő és a \(\displaystyle P\) pont elmozdulása közötti kapcsolat:
\(\displaystyle F(x)=F_1-F_2=D\left(\frac{\ell}{\ell_1}+\frac{\ell}{\ell_2}\right) x.\)
Megjegyzés: A megfeszített rugó éppen úgy viselkedik, mint egy \(\displaystyle D\) rugóállandójú, \(\displaystyle \ell\) hosszúságú, kezdetben feszítetlen rugó. Ez utóbbi azonban húzó-nyomó rugó kell hogy legyen, hiszen az alsó rugó függőlegesen lefelé ható erő esetén megrövidül, benne nyomófeszültségek alakulnak ki. Az előfeszítés azt eredményezi, hogy a könnyebben megvalósítható ,,húzó'' rugóval is létrehozható (nem túl nagy deformációk esetén) úgy a felfelé, mind pedig a lefelé ható eredő erő.
A továbbiakban vizsgáljuk meg, mekkora \(\displaystyle x\) távolsággal süllyed le a rugó felezőpontja felett \(\displaystyle y\) távolságban elhelyezett \(\displaystyle mg\) súlyú test (a denevér) az egyensúlyi állapotában. Ilyenkor
\(\displaystyle \ell_1=\frac{\ell}{2}-y,\qquad \ell_2=\frac{\ell}{2}+y,\)
az egyensúly feltétele tehát
\(\displaystyle D\ell\left(\frac{1}{\frac{\ell}{2}-y }+\frac{1}{\frac{\ell}{2}+y }\right) x=mg,\)
vagyis
\(\displaystyle \ell x=\frac{mg}{D\ell}\left(\frac{\ell^2}{4}-y^2\right).\)
Célszerű bevezetni a dimenziótlan
| \(\displaystyle (1)\) | \(\displaystyle \lambda \equiv\frac{mg}{D\ell}\) |
jelölést, ezzel az \(\displaystyle y\) és \(\displaystyle x\) közötti kapcsolat:
| \(\displaystyle (2)\) | \(\displaystyle x=\lambda\frac{\ell}{4}-\lambda\frac{y^2}{\ell}.\) |
\(\displaystyle a)\) Ha \(\displaystyle \ell/2\) magasan lévő pontba repül a denevér, ami az \(\displaystyle y=0\) esetnek felel meg, akkor az egyensúly beállta után (1) és (2) szerint
| \(\displaystyle (3)\) | \(\displaystyle x=\frac{\lambda}{4}\ell=\frac{mg}{4D}\) |
távolsággal kerül lejjebb.
Megjegyzés. Feltételeztük, hogy \(\displaystyle x<(\ell-d)/2\) (vagyis a rugó előfeszítettsége elegendően nagy, és így a denevér alatt lévő rugódarab még az egyensúlyi állapotban is feszes marad).
\(\displaystyle b)\) Ha a denevér nagyon lassan, óvatosan felmászik a rugónak egy olyan \(\displaystyle P\) pontjába, amely – ha a deformáltság a rugó mentén mindenhol ugyanakkora lenne – \(\displaystyle y\) távolsággal lenne magasabban a felezőpontnál, és onnan éppen \(\displaystyle x=y\) távolsággal süllyed le, akkor a talajtól mért távolsága továbbra is \(\displaystyle \ell/2\) maradna. A (2) egyenlet számunkra érdekes \(\displaystyle y>0\) megoldása \(\displaystyle x=y\) esetén:
| \(\displaystyle (4)\) | \(\displaystyle y=\frac{\ell}{2\lambda}\left(\sqrt{1+\lambda^2}-1\right)=\frac{D\ell^2}{2mg}\left(\sqrt{1+\frac{m^2g^2}{D^2\ell^2}}-1\right).\) |
Megjegyzés: Ha a rugó a denevér súlyához képest viszonylag erős, vagyis \(\displaystyle D\ell \gg mg,\) akkor \(\displaystyle y\ll \ell\) és \(\displaystyle D_1\approx D_2\approx 2D\), a denevér által okozott rugómegnyúlás \(\displaystyle y\approx mg/(4D)\), ami éppen az \(\displaystyle a)\) alkérdésben szereplő \(\displaystyle x\)-szel egyenlő.
A denevér mászása közben az egész rendszer energiájának megváltozása (a denevér gravitációs helyzeti energiájának változása és a rugók rugalmas energiájának változása) így adható meg:
\(\displaystyle \Delta E=mgx+\frac{1}{2}\left(D_1+D_2\right)\,y^2-\frac{1}{2}\left(2D\right)\,2x^2= \frac{(mg)^2}{8D}+\frac{D\ell^2}{4}\left(\sqrt{1+\frac{m^2g^2}{D^2\ell^2}}-1\right).\)
Erős rugó határesetben \(\displaystyle \Delta E={m^2g^2}/(4D).\)
Megjegyzés: A mechanikai energiaváltozást az egyszerűbb
\(\displaystyle \Delta E=\frac{mg}{2}(x+y)\)
képlet alapján is ki lehet számítani, ahol \(\displaystyle x\)-et és \(\displaystyle y\)-t természetesen ki kell fejezni (3).nak és (4)-nek megfelelően \(\displaystyle D\), \(\displaystyle mg\) és \(\displaystyle \ell\) segítségével. A képlet szemléletes jelentése a következő. A denevér és a rugórendszer kezdeti energiája az \(\displaystyle \ell/2\) magasságból \(\displaystyle x\) távolságnyit lassan (gyorsulásmentesen) lesüllyesztett testen végzett munkával egyenlő. (A rugalmas energiát a terheletlen, de megfelelően előfeszített állapotban választjuk nullának, a helyzeti energia nullpontját pedig a rugó felezőpontjához igazítjuk.) A végzett munka az átlagos \(\displaystyle mg/2\) erő és az \(\displaystyle x\) elmozdulás előjeles szorzata: \(\displaystyle -mgx/2.\) A felmászás utáni állapot rugalmas energiája azzal a munkával egyenlő, amennyivel a rugó megfelelő \(\displaystyle P\) pontját lassan \(\displaystyle y\) távolsággal lejjebb tudjuk húzni. Ez ismét az átlagos húzóerőből számítható: \(\displaystyle mgy/2\). A két energia különbsége a denevér által előidézett mechanikai energiaváltozás.
A denevér által végzett munka legalább akkora, mint a mechanikai energia növekedése. Ennél azonban nagyobb is lehet, ha a denevér gyorsan, vagy ugrásszerűen mozog, hiszen ekkor a rugóban rugalmas hullámok keletkezhetnek, amelyek lecsillapodása során hő fejlődik.
Statistics:
22 students sent a solution. 5 points: Markó Gábor, Marozsák Tádé. 4 points: Lipták Gergő, Merkl Gergely, Olosz Adél, Sas 202 Mór, Varga Vázsony. 3 points: 5 students. 2 points: 3 students. 1 point: 5 students. 0 point: 2 students.
Problems in Physics of KöMaL, November 2018
