Problem P. 5073. (November 2018)

P. 5073. The linear charge density of a vertical very long (``infinitely'' long) straight insulating thread is \(\displaystyle \lambda=8\cdot10^{-7}\) C/m. A small metal ball of mass \(\displaystyle m=2\) g and of charge \(\displaystyle q=7\cdot10^{-8}\) C, is hung by a very thin insulating filament of length \(\displaystyle \ell=10\) cm, at a distance of \(\displaystyle d_0=5~\)cm from the thread. Without any push the ball is released when the filament is vertical.

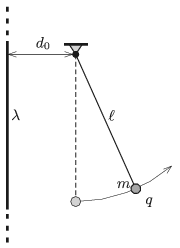
\(\displaystyle a)\) How far will the metal ball move from the thread?

\(\displaystyle b)\) What is the angle between the vertical and the filament when the ball moves at its maximum speed? What is this maximum speed?

\(\displaystyle c)\) What force is exerted on the support when the ball is moving at its greatest speed?

(5 pont)

Deadline expired on December 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A szigetelőszál körül az elektromos térerősség ,,radiális'', és a nagysága a száltól \(\displaystyle r\) távolságban (az elektrosztatikai Gauss-törvény szerint)

\(\displaystyle E(r)=\frac{2k\lambda}{r}.\)

Ez a térerősség az

\(\displaystyle U(r)=- 2k\lambda \ln \frac{r}{r_0} \)

potenciálnak felel meg, amint az integrálszámítással, vagy a hőtani analógia alapján (az izotermikus munkavégzés képlete alapján) látható be. A potenciál nullpontját önkényesen választott \(\displaystyle r_0\) távolsághoz illesztettük, ez a távolság lehet például a fonál függőleges helyzetének megfelelő \(\displaystyle d_0\) érték.

Jelöljük a fonál függőlegessel bezárt szögét \(\displaystyle x\)-szel, és alkalmazzuk az energiamegmaradás tételét! Mivel a szigetelőszáltól mért távolság

\(\displaystyle d=d_0+\ell\sin x,\)

fennáll

\(\displaystyle \frac{1}{2}mv^2+mg\ell(1-\cos x)-2kq\lambda \ln \frac{d}{d_0}=0,\)

vagyis

\(\displaystyle f(x)\equiv v^2(x)=\frac{4kq\lambda}{m}\, \ln\left( 1+\frac{\ell}{d_0}\sin x\right)-2g\ell(1-\cos x).\)

A megadott mennyiségeket behelyettesítve (SI-egységrendszerben számolva)

\(\displaystyle f(x)=\ln\left( 1+2\sin x\right)-1{,}96\,(1-\cos x).\)

\(\displaystyle a)\) A fémgolyó legnagyobb eltávolodását, vagyis a megállását jellemző szöget az \(\displaystyle f(x)=0\) egyenlet \(\displaystyle (x>0)\) gyöke adja meg. Grafikus ábrázolással, vagy pl. a http://www.wolframalpha.com segítségével megkaphatjuk, hogy \(\displaystyle x\approx 1{,}05 \) rad, azaz kb. \(\displaystyle 60^\circ\). Ennek megfelelően a fémgömb legfeljebb 13,7 cm-re távolodik el a szigetelőszáltól.

\(\displaystyle b)\) Ugyancsak az \(\displaystyle f(x)\) függvény vizsgálatával, a maximumának megkeresésével kapjuk meg a sebesség legnagyobb értékét. Ez \(\displaystyle x\approx 0{,}49\) radiánnál, azaz \(\displaystyle 28^\circ\)-nál található, és \(\displaystyle v_\text{max}=0{,}66~\)m/s.

\(\displaystyle c)\) A legnagyobb sebességnél a fonalat feszítő erő (Newton mozgástörvénye alapján):

\(\displaystyle F=mg\cos x+\frac{mv_\text{max}^2}{\ell}+\frac{2k\lambda q}{d_0+\ell\sin x}\sin x \approx 0{,}03~\rm N.\)

Statistics:

29 students sent a solution.
5 points:	Bekes Barnabás, Békési Ábel, Csépányi István, Makovsky Mihály, Máth Benedek, Molnár Mátyás, Olosz Adél, Sal Dávid, Tiefenbeck Flórián.
4 points:	Bokor Endre, Elek Péter, Jánosik Áron, Ludányi Levente, Marozsák Tádé, Németh Csaba Tibor, Pácsonyi Péter, Vass Bence, Viczián Anna.
3 points:	5 students.
2 points:	3 students.
1 point:	2 students.
0 point:	1 student.

Problems in Physics of KöMaL, November 2018