 Problem P. 5077. (November 2018)
Problem P. 5077. (November 2018)
P. 5077. There is a piston having good thermal conductivity in the middle of a cuboid-shaped container having thermally insulating walls. On the left side of the piston there is a sample of air of volume \(\displaystyle V_0\), whilst on the right side there is a sample of air of volume \(\displaystyle V_0/2\) at a pressure of \(\displaystyle p_0=76~{\rm Hgcm}\approx 10^5\) Pa, and a mercury column of height \(\displaystyle h=38~\)cm. The total width of the container is \(\displaystyle 2h\) (not considering the width of the piston), and its height is also \(\displaystyle 2h\).
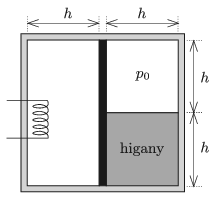
By means of a built-in electric heater the left side of the system is slowly heated. The temperatures of the two samples of gases are the same at any time. At most what can the displacement of the piston be, if the expansion of the container, the piston and the mercury is neglected?
(6 pont)
Deadline expired on December 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a bal oldali részben lévő levegő kezdeti nyomását \(\displaystyle p_1\)-gyel (1. ábra), és számítsuk ki ennek nagyságát a dugattyú egyensúlyi feltételéből! Mivel (a megadott számadatok esetén) \(\displaystyle h\) magas higany hidrosztatikai nyomása éppen \(\displaystyle p_0/2\), a higany tetején a nyomás \(\displaystyle p_0\), a legalján pedig \(\displaystyle \tfrac 32 p_0\), így a higany átlagos nyomása \(\displaystyle \tfrac 54 p_0\). A dugattyú mélysége (az ábra síkjára merőleges irányú kiterjedése) \(\displaystyle \ell=V_0/(2h^2)\), de ez a mennyiség a továbbiakban érdektelen, minden képletből kiesik. A dugattyúra ható erők egyensúlyának feltétele:
| \(\displaystyle (1)\) | \(\displaystyle p_1\, 2h=p_0 \, h+\tfrac 54 p_0\cdot h,\qquad \text{azaz}\qquad p_1=\frac{9}{8}p_0.\) |
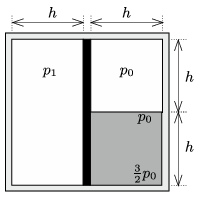
1. ábra
A két térfélben a levegő hőmérséklete ugyanakkora, hiszen a dugattyú anyaga jó hővezető. Ez a feltétel meghatározza a két gázmennyiség mólszámának arányát (ami a továbbiakban nyilván nem változik):
| \(\displaystyle (2)\) | \(\displaystyle \frac {n_\text{bal}}{n_\text{jobb}}=\frac{2h^2\cdot p_1}{ h^2\cdot p_0}=\frac{9}{4}.\) |
A fűtőszál bekapcsolása után a bal oldali térfélben is, és a jobb oldali részben is lassan felmelegszik a levegő (és vele együtt a higany is). Mindkét oldalon nő a levegő nyomása (ezek jelölése a 2. ábrán látható), és a dugattyú elmozdul valamekkora \(\displaystyle xh\) távolsággal. A higany (jó közelítéssel) összenyomhatatlan, emiatt a szintje valamekkora \(\displaystyle yh\) értékig megemelkedik, amint azt a 2. ábra mutatja. A higany átlagos nyomása (a teteje és az alja nyomásának számtani közepe): \(\displaystyle p_3+(y/4)p_0.\)
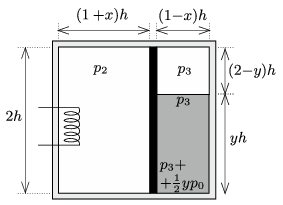
2. ábra
Tekintsünk most valamekkora \(\displaystyle x\) értékhez (elmozdulás-arányszámhoz) tartozó állapotot! A következő egyenleteket írhatjuk fel:
\(\displaystyle 2p_2h=p_3(2-y)h+(p_3+\frac{yp_0}{4})yh, \)
vagyis
| \(\displaystyle (3)\) | \(\displaystyle p_2=p_3+\frac{y^2}{8}p_0,\) |
továbbá a higany térfogatának állandósága miatt
| \(\displaystyle (4)\) | \(\displaystyle y(1-x)=1,\) |
és végül a gáztörvény szerint
| \(\displaystyle (5)\) | \(\displaystyle \frac{2p_2(1+x)}{p_3(2-y)(1-x)}=\frac {n_\text{bal}}{n_\text{jobb}}.\) |
Az (1)-(5) egyenletekből kifejezhetjük a két levegőrész nyomását, illetve a higanyszint magasságát \(\displaystyle x\) függvényében, és ezekből kiszámíthatjuk a rendszer energiájának megváltozását, ami a fűtőszál által leadott hővel egyenlő.
\(\displaystyle p_2=\frac{9(1-2x)}{8(1-x)^2(1-26x)}p_0,\)
\(\displaystyle p_3=\frac{1+x}{(1-x)^2(1-26x)}p_0.\)
Ha az \(\displaystyle x\) arányszám 0-tól indulva lassan növekszik, a két levegőrész nyomása fokozatosan emelkedik, és \(\displaystyle x\rightarrow \tfrac1{26}\) határesetben mindkettő végtelenhez tart, miközben a térfogatok és a higanyoszlop magassága véges nagyságú marad. Ez annyit jelent, hogy a rendszer energiájának akármilyen mértékű növelésével is legfeljebb \(\displaystyle x_{\rm max}h=\tfrac1{26}h\approx 15~\)mm-t mozdulhat el.
Megjegyzés. Reális körülmények között természetesen a határesetet megközelítő, vagy azt elérő elmozdulás ténylegesen nem következhet be, hiszen a korlátlanul növekvő nyomás és hőmérséklet hatására a tartály vagy szétrobban, vagy megolvad. Elég magas hőmérsékleten a higanygőz nyomása is számottevővé válik, a dugattyúra ható erők egyensúlyánál azt is figyelembe kell venni.
Statistics:
23 students sent a solution. 6 points: Bokor Endre, Csépányi István, Elek Péter, Fülöp Sámuel Sihombing, Markó Gábor, Marozsák Tádé, Olosz Adél, Sal Dávid, Tiefenbeck Flórián. 5 points: Vaszary Tamás. 4 points: 1 student. 3 points: 4 students. 2 points: 5 students. Unfair, not evaluated: 3 solutionss.
Problems in Physics of KöMaL, November 2018
