 Problem P. 5090. (January 2019)
Problem P. 5090. (January 2019)
P. 5090. There is a cube-shaped box of mass \(\displaystyle m\) on a horizontal floor. A thin, uniform rod of also mass \(\displaystyle m\) is leant against one of the faces of the cube touching it at its centre. Initially both of the objects are fixed. The angle between the ground and the rod is \(\displaystyle \alpha=45^\circ\).
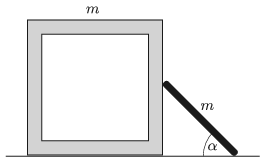
What is the initial acceleration of the box at which it starts to move when the objects are released? (Friction is negligible everywhere.)
(5 pont)
Deadline expired on February 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Vegyük fel az egyes testekre ható erőket és a testek gyorsulását (szöggyorsulását) az 1. ábrán látható módon. Itt már kihasználtuk, hogy a tömegközépponti tétel értelmében a doboz és pálca tömegközéppontjának vízszintes gyorsulása egyenlő nagyságú, de ellentétes irányú.
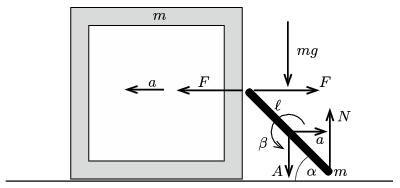
1. ábra
A mozgásegyenletek:
| \(\displaystyle (1)\) | \(\displaystyle F=ma,\) |
| \(\displaystyle (2)\) | \(\displaystyle mg-N=mA,\) |
| \(\displaystyle (3)\) | \(\displaystyle N\frac{\ell}{2\sqrt2}-F\frac{\ell}{2\sqrt2}=\frac{m\ell^2}{12}\beta.\) |
Ezekhez a mozgásegyenletekhez két kényszerfeltétel (a pálca felső végének vízszintes irányú gyorsulására és az alsó végének függőleges irányú gyorsulására vonatkozó megszorítás) járul:
| \(\displaystyle (4)\) | \(\displaystyle a-\frac{\ell}{2}\beta \frac{1}{\sqrt2}=-a,\) |
| \(\displaystyle (5)\) | \(\displaystyle \frac{\ell}{2}\beta \frac{1}{\sqrt2}=A.\) |
Az (1)-(5) egyenletből az öt ismeretlen (\(\displaystyle F\), \(\displaystyle N\), \(\displaystyle a\), \(\displaystyle A\) és \(\displaystyle \beta\)) meghatározható, és a doboz keresett gyorsulására az
\(\displaystyle a=\frac{3}{13}g\)
eredmény adódik.
II. megoldás. Számítsuk ki az energiamegmaradás törvényének felhasználásával, hogy mekkora sebességre gyorsul fel a doboz az indítást követő nagyon rövid \(\displaystyle t\) idő alatt. Ha a testek sebessége (szögsebessége) a 2. ábrán látható nagyságú, akkor az energiatétel szerint
| \(\displaystyle (6)\) | \(\displaystyle \frac{1}{2}mv^2+\frac{1}{2}m\left(v^2+u^2\right)+\frac{1}{2}\, \frac{m\ell^2}{12}\omega^2=mgh,\) |
ahol \(\displaystyle h\) a pálca tömegközéppontjának lesüllyedése \(\displaystyle t\) idő alatt.
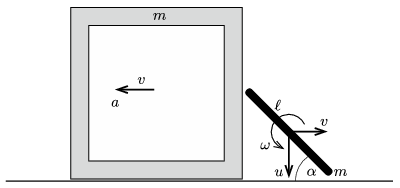
2. ábra
A kényszerfeltételek (miszerint a pálca végpontjai nem távolodnak el a doboztól, illetve a talajtól):
| \(\displaystyle (7)\) | \(\displaystyle \frac{\ell}{2}\omega \frac{1}{\sqrt2}-v=v,\) |
| \(\displaystyle (8)\) | \(\displaystyle \frac{\ell}{2}\omega \frac{1}{\sqrt2}-u=0.\) |
A (6)-(8) egyenletből (\(\displaystyle \beta\) kiküszöbölése után)
| \(\displaystyle (9)\) | \(\displaystyle \frac{26}{3}v^2=2gh\qquad \text{és} \qquad u=2v\) |
adódik.
Az indulást követő nagyon rövid idő alatt a doboz mozgása \(\displaystyle a\) gyorsulású egyenletesen változó mozgásnak tekinthető, és így a
\(\displaystyle v=at,\qquad \text{valamint} \qquad h=\frac{1}{2}ut=vt=at^2\)
összefüggések teljesülnek. Ezeket (9)-be helyettesítve a
\(\displaystyle \frac{26}{3}a^2t^2=2g\cdot at^2,\)
vagyis az
\(\displaystyle a=\frac{3}{13}g\)
végeredményt kapjuk.
Megjegyzés. Az energiamegmaradásra hivatkozó megoldás azért kényelmes, mert nincs szükség a belső erők (\(\displaystyle N\) és \(\displaystyle F\)) felvételére, hiszen ezek munkavégzése nulla.
Statistics:
40 students sent a solution. 5 points: Bekes Barnabás, Csépányi István, Elek Péter, Hartmann Alice, Havasi Márton, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Merkl Gergely, Olosz Adél, Sal Dávid, Szabó 314 László, Vass Bence. 4 points: Bokor Endre, Sepsi Csombor Márton, Tiefenbeck Flórián. 3 points: 5 students. 2 points: 1 student. 1 point: 18 students.
Problems in Physics of KöMaL, January 2019
