 Problem P. 5099. (January 2019)
Problem P. 5099. (January 2019)
P. 5099. A roller coaster car is moving along a vertical circular loop such that it uses its own engine and brakes to keep its speed constant. What should its least speed be in order that it follows the circular loop of radius \(\displaystyle R\) without slipping, if the coefficient of static friction is \(\displaystyle \mu\)? Where would it slip if its speed was a bit smaller than this value? The car is small enough compared to the radius of the loop.
(6 pont)
Deadline expired on February 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük az \(\displaystyle m\) tömegű kocsi (állandó) sebességét \(\displaystyle v_0\)-lal, a sínek által kifejtett, sugárirányú nyomóerőt \(\displaystyle N\)-nel, az érintő irányú súrlódási erőt \(\displaystyle S\)-sel, és a kocsi pillanatnyi helyzetét adjuk meg az 1. ábrán látható \(\displaystyle \varphi\) szöggel. Legyen a kocsi tömege \(\displaystyle m\), a rá ható nehézségi erő tehát \(\displaystyle mg\).
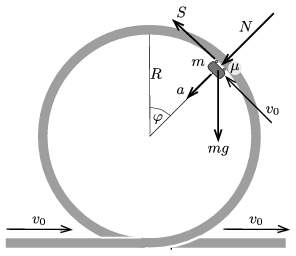
1. ábra
A kocsi egyenletes körmozgást végez, a gyorsulása tehát a pálya középpontja felé mutató,
\(\displaystyle a=\frac{v_0^2}{R}\)
nagyságú vektor. A Newton-féle mozgásegyenletek:
\(\displaystyle mg\sin\varphi-S=0,\)
\(\displaystyle mg\cos\varphi+N=m\frac{v_0^2}{R},\)
ahonnan
| \(\displaystyle (1)\) | \(\displaystyle S=mg\sin\varphi,\) |
| \(\displaystyle (2)\) | \(\displaystyle N=m\frac{v_0^2}{R}-mg\cos\varphi.\) |
A kocsi akkor nem csúszik meg a sínen, ha a pálya minden pontjában (vagyis minden \(\displaystyle \varphi\) szögnél) teljesül, hogy
| \(\displaystyle (3)\) | \(\displaystyle \mu>\frac{\vert S\vert}{N}\equiv \frac{\vert\sin\varphi\vert}{k-\cos\varphi},\) |
ahol
\(\displaystyle k=\frac{v_0^2}{Rg}\)
a sebesség nagyságára jellemző dimenziótlan szám. Az \(\displaystyle N\) nyomóerő legkisebb értékét a pálya legmagasabb pontjában, \(\displaystyle \varphi=0\)-nál éri el. Nyilván még itt is teljesülnie kell az \(\displaystyle N>0\) feltételnek (ellenkező esetben a kocsi elválik a sínektől), vagyis (2) alapján
\(\displaystyle m\frac{v_0^2}{R}>mg, \qquad \text{azaz}\qquad k>1.\)
Ahhoz, hogy a kocsi semelyik \(\displaystyle \varphi\) szögnél ne csússzon meg, a tapadó súrlódási együttható nagyobb kell, hogy legyen
| \(\displaystyle (4)\) | \(\displaystyle f(\varphi)\equiv \frac{\sin\varphi}{k-\cos\varphi} \) |
legnagyobb értékénél. Ha (3) éppen nem teljesülne (vagyis \(\displaystyle v_0\) egy ,,kicsit kisebb'' lenne a kritikus értéknél, akkor a kocsi az \(\displaystyle f(\varphi)\) függvény maximumához tartozó \(\displaystyle \varphi_0\) szög közelében megcsúszna. Feladatunk tehát a továbbiakban a (4)-ben megadott \(\displaystyle f(\varphi)\) függvény maximumhelyének és a maximum nagyságának meghatározása.
Megjegyzés. Elegendő a \(\displaystyle 0\le\varphi\le 180^\circ\) tartományban vizsgálódnunk, ekkor a kocsi ,felfelé'' halad. A ,,lefelé'' mozgó kocsinál, amikor \(\displaystyle -180^\circ\le\varphi\le 0\), a csúszásmentes mozgás feltétele ugyanaz, mint a felfelé haladó kocsinál, hiszen \(\displaystyle S(-\varphi)=-S(\varphi)\) és \(\displaystyle N(-\varphi)=N(\varphi)\).)
Ennek a (matematikai) problémának többféle módon is nekikezdhetünk:
I. (geometriai) módszer. Tekintsünk egy egységnyi hosszúságú pálcát, amelyet egy vízszintes egyenesre fektettünk. + A pálcát az egyik \(\displaystyle (P)\) végpontja körül \(\displaystyle \varphi\) szöggel elforgatjuk (2. ábra).
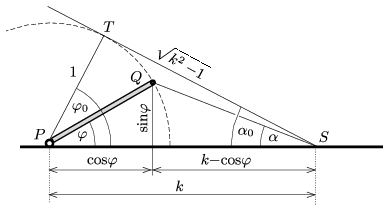
2. ábra
Ha a vízszintes egyenesre illeszkedő, a forgásponttól \(\displaystyle k\) távolságban található \(\displaystyle S\) pontból szemléljük a pálca másik \(\displaystyle (Q)\) végpontját, azt a vízszinteshez képest
\(\displaystyle \alpha=\arctg\frac{\sin\varphi}{k-\cos\varphi}\equiv \arctg f(\varphi)\)
szögben látjuk. Az \(\displaystyle \alpha\) hegyesszög legnagyobb értéke \(\displaystyle f(\varphi)\) maximális értékét is megadja:
\(\displaystyle (\tg\alpha)_\text{max}=f_\text{max},\)
és a maximum helyét is meghatározza:
\(\displaystyle f\left(\varphi_0\right)= f_\text{max}.\)
Mivel a pálca forgatása közben a \(\displaystyle Q\) pont egy körív mentén mozog, \(\displaystyle \alpha\) legnagyobb értékét akkor kapjuk, amikor \(\displaystyle ST\) érinti ezt a kört, vagyis a \(\displaystyle PTS\) háromszög derékszögű. Innen következik, hogy
| \(\displaystyle (5)\) | \(\displaystyle \cos\varphi_0=\frac{1}{k},\) |
továbbá
\(\displaystyle f_\text{max}=\tg\alpha_0=\frac{1}{\sqrt{k^2-1}}.\)
A hullámvasút kocsija tehát akkor tud csúszásmentesen végighaladni a függőleges síkú körpályán, ha
| \(\displaystyle (6)\) | \(\displaystyle \mu>\frac{1}{\sqrt{k^2-1}},\) |
illetve ennek megfordítása,
\(\displaystyle k=\frac{v_0^2}{Rg}>\sqrt{\frac{1}{\mu^2}+1}\)
teljesül.
II. (trigonometriai) módszer. A meg nem csúszás (3) feltétele az \(\displaystyle \varepsilon\) súrlódási határszög (\(\displaystyle \mu=\tg\varepsilon\)) bevezetésével így írható fel:
\(\displaystyle \frac{\sin\varepsilon}{\cos\varepsilon}>\frac{\sin\varphi}{k-\cos\varphi},\)
vagyis
\(\displaystyle k\sin\varepsilon >\sin\varphi\cos\varepsilon+\cos\varphi\sin\varepsilon, \)
azaz
| \(\displaystyle (7)\) | \(\displaystyle k\sin\varepsilon>\sin(\varphi+\varepsilon).\) |
Ez az egyenlőtlenség biztosan teljesül, ha
| \(\displaystyle (8)\) | \(\displaystyle \sin\varepsilon>\frac{1}{k},\) |
azaz
\(\displaystyle \mu=\tg\varepsilon=\frac{1}{\sqrt{\frac{1}{\sin^2\varepsilon}-1}}>\frac{1}{\sqrt{k^2-1}}. \)
Ez éppen a (6) egyenlőtlenség.
Amennyiben (6) éppen nem teljesül (vagyis \(\displaystyle \sin\varepsilon\approx (1/k)\)), akkor \(\displaystyle \varphi=\varphi_0\approx 90^\circ-\varepsilon\) szögnél a kocsi megcsúszik, hiszen itt válik a (7) egyenlőtlenség élessé. A megcsúszás helyét így is megadhatjuk:
\(\displaystyle \cos\varphi_0=\sin\varepsilon\approx \frac{1}{k},\)
összhangban a geometriai módszerrel kapott (5) összefüggéssel.
III. (differenciálszámításos) módszer. A (4) képlettel megadott függvény szélsőértékét (maximumát) a deriváltjának eltűnéséből is meg lehet kapni:
\(\displaystyle f'(\varphi)=\frac{(k-\cos\varphi)\cos\varphi-\sin^2\varphi}{(k-\cos\varphi)^2} \equiv \frac{k\cos\varphi-1}{(k-\cos\varphi)^2}=0.\)
Ez akkor teljesül, ha
\(\displaystyle \varphi=\varphi_0\qquad \text{ahol}\qquad \cos\varphi_0=\frac{1}{k},\)
továbbá
\(\displaystyle f_\text{max}=f(x_0)=\frac{1}{\sqrt{k^2-1}},\)
ahogy azt már korábban is megkaptuk.
Érdemes megvizsgálni két szélsőséges esetet. Ha \(\displaystyle \mu\gg 1\), vagyis a tapadó súrlódás igen nagy (ezt pl. a fogaskerekes megoldás valósítja meg legjobban), akkor a kritikus helyzetben (a megcsúszás határhelyzetében) \(\displaystyle v_0\approx \sqrt{Rg}\) és \(\displaystyle \varphi_0\approx 0\). A vonat tehát olyan lassan mozoghat, hogy a pálya tetőpontjánál majdnem leesik, és a megcsúszás is itt, a tetőpont közelében következik be, ha a sebesség egy kicsivel alacsonyabb a szükségesnél.
Ha viszont \(\displaystyle \mu\ll 1\) (a pálya nagyon csúszós), akkor \(\displaystyle v_0\gg \sqrt{Rg}\) (tehát a vonatnak igen gyorsan kell haladnia), és ha mégis megcsúszik, az \(\displaystyle \varphi_0\approx 90^\circ\)-nál, vagyis a pálya függőleges szakaszánál fog bekövetkezni.
Statistics:
24 students sent a solution. 6 points: Andorfi István, Bokor Endre, Csépányi István, Hisham Mohammed Almalki, Mácsai Dániel, Markó Gábor, Máth Benedek, Olosz Adél, Sal Dávid, Szabó 314 László, Tiefenbeck Flórián, Varga Vázsony. 5 points: Hervay Bence, Marozsák Tádé. 4 points: 4 students. 2 points: 2 students. 1 point: 4 students.
Problems in Physics of KöMaL, January 2019
