 Problem P. 5121. (March 2019)
Problem P. 5121. (March 2019)
P. 5121. Three small alike balls (denoted by the letters \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\)) of mass \(\displaystyle m\) are attached by means of two negligible-mass rods of length \(\displaystyle \ell\), such that one of the rods joins balls \(\displaystyle A\) and \(\displaystyle B\), whilst the other joins balls \(\displaystyle B\) and \(\displaystyle C\). At ball \(\displaystyle B\) there is an articulate joint so the angle between the rods can be freely varied. The system is at rest in weightlessness, and the three balls are collinear. Then at an instant an initial velocity of \(\displaystyle v_0\) is given to ball \(\displaystyle A\) perpendicularly to the rods. What are the forces in the rods at the moment right after starting ball \(\displaystyle A\)?
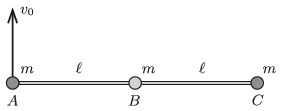
(6 pont)
Deadline expired on April 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Az egyes rudakra ható erők eredője és a forgatónyomatékuk eredője nulla, hiszen a rudak tömege (és ezzel együtt a tehetetlenségi nyomatékuk is) elhanyagolható. Ez a feltétel csak akkor teljesülhet, ha a rudak végeinél egyenlő nagyságú, a rúddal párhuzamos, de ellentétes irányú erők hatnak. Jelöljük az \(\displaystyle A\) és \(\displaystyle B\) golyó közötti rúdban ható erőt \(\displaystyle F\)-fel, a \(\displaystyle B\) és \(\displaystyle C\) golyók közötti rúdban hatót pedig \(\displaystyle K\)-val! Az egyes golyókra ható erőket és a kezdeti gyorsulásokat az 1. ábra mutatja.
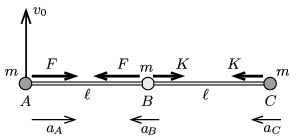
1. ábra
A golyók gyorsulása (Newton törvénye szerint)
| \(\displaystyle (1)\) | \(\displaystyle a_A=\frac{F}{m}; \qquad a_B=\frac{F-K}{m}; \qquad a_C=\frac{K}{m}.\) |
Mindhárom gyorsulás rúdirányú, hiszen a golyókra ható erők is ilyenek.
A jobb oldali rúd hossza nem változhat meg, emiatt \(\displaystyle a_B=a_C\), azaz
| \(\displaystyle (2)\) | \(\displaystyle F=2K. \) |
Tekintsük most a bal oldali rudat és a végeinél lévő \(\displaystyle A\) és \(\displaystyle B\) golyókat (2. ábra)! Erre az alrendszerre összesen \(\displaystyle F+(K-F)=K\) erő hat, emiatt a tömegközéppontjának (a rúd középpontjának) a gyorsulása
\(\displaystyle a_{\rm tkp}=\frac{K}{2m}.\)
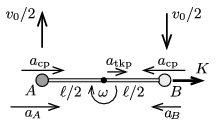
2. ábra
A rúd tömegközéppontjának sebessége az indítás utáni pillanatokban \(\displaystyle v_0/2\). A rúd forgómozgást is végez a középpontja körül, az \(\displaystyle A\) golyó \(\displaystyle v_0/2\) sebességgel mozog a tömegközépponthoz képest ,,előrefelé'' (hiszen a teljes sebessége \(\displaystyle v_0\)), a \(\displaystyle B\) golyó pedig ,,visszafelé'' mozog \(\displaystyle v_0/2\) sebességgel, az eredő sebessége nulla.
A rúd szögsebessége ezek szerint
\(\displaystyle \omega=\frac{\left(v_0/2\right)}{\left(\ell/2\right)} =\frac{v_0}{\ell}.\)
Ugyanezt az eredményt úgy is megkaphatjuk, hogy a rúd forgását eredeti (tehát nem a tömegközépponti) rendszerben írjuk le. Az \(\displaystyle \ell\) hosszúságú rúd \(\displaystyle B\) pontja kezdetben áll, az \(\displaystyle A\) pontja \(\displaystyle v_0\) sebességgel mozog, a rúd szögsebessége tehát (bármelyik inerciarendszerben) \(\displaystyle v_0/\ell\).
A rúd végpontjainak centripetális gyorsulása
\(\displaystyle a_{\rm cp}= \frac{\ell}{2}\omega^2=\frac{v_0^2}{2\ell}.\)
Az \(\displaystyle A\) golyó gyorsulása:
\(\displaystyle a_A=a_{\rm tkp}+a_{\rm cp}=\frac{K}{2m}+\frac{v_0^2}{2\ell}.\)
Innen (1)-t, majd a (2) összefüggést felhasználva:
\(\displaystyle \frac{F}{m}=\frac{K}{2m}+\frac{v_0^2}{2\ell},\)
\(\displaystyle \frac{2K}{m}=\frac{K}{2m}+\frac{v_0^2}{2\ell} \)
adódik, ahonnan a keresett rúderők:
\(\displaystyle K=\frac13\, \frac{mv_0^2}{\ell}; \qquad F=\frac23\,\frac{mv_0^2}{\ell}.\)
II. megoldás. Az I. megoldás jelöléseit követve felírhatjuk, hogy az egyes golyók gyorsulása
| \(\displaystyle (1)\) | \(\displaystyle a_A=\frac{F}{m}; \qquad a_B=\frac{F-K}{m}; \qquad a_C=\frac{K}{m}.\) |
Tekintsük az indítást követő \(\displaystyle t\) idő alatti elmozdulásokat! Legyen \(\displaystyle t\) olyan kicsiny, hogy a négyzeténél magasabb hatványait már elhanyagolhassuk. Az \(\displaystyle A\) golyó (az 1. ábrát nézve) ,,felfelé'' közelítőleg
\(\displaystyle y_1=v_0t\)
távolsággal, jobbra pedig
\(\displaystyle x_1=\frac{F}{2m}t^2\)
távolsággal mozdul el. Hasonló módon érvelve a \(\displaystyle B\) golyó balra mozdul el
\(\displaystyle x_2=\frac{F-K}{2m}t^2\)
távolságnyit. (A közelítés annak felel meg, hogy a golyók mozgását egyenletesen gyorsulónak tekintjük a mozgás kezdeti, rövid szakaszán.) A bal oldali rúd hossza nem változhat meg, tehát
\(\displaystyle \left( \ell-x_1-x_2\right)^2+y_1^2=\ell^2,\)
azaz (a \(\displaystyle t^2\)-nél magasabb hatványokat elhanyagolva)
\(\displaystyle \ell^2-2\ell\left(\frac{F}{2m}t^2+\frac{F-K}{2m}t^2\right)+v_0^2t^2=\ell^2,\)
ahonnan
| \(\displaystyle (3)\) | \(\displaystyle 2F-K=\frac{mv_0^2}{\ell}.\) |
Hasonló módon kapjuk, hogy a jobb oldali rúd hossza akkor maradhat csak állandó, ha
\(\displaystyle a_B\frac{t^2}{2}-a_C\frac{t^2}{2}=0,\)
vagyis
| \(\displaystyle (4)\) | \(\displaystyle 2K-F=0.\) |
A (3) és (4) egyenletekből kapjuk, hogy
\(\displaystyle K=\frac13\, \frac{mv_0^2}{\ell}; \qquad F=\frac23\,\frac{mv_0^2}{\ell}.\)
Statistics:
7 students sent a solution. 6 points: Elek Péter, Marozsák Tádé, Olosz Adél. 5 points: Békési Ábel. 3 points: 2 students. 0 point: 1 student.
Problems in Physics of KöMaL, March 2019
