 Problem P. 5125. (April 2019)
Problem P. 5125. (April 2019)
P. 5125. A slope of angle of elevation of \(\displaystyle \alpha =30^\circ\) is followed by a cylindrical surface of radius \(\displaystyle R=32~\)cm as shown in the figure. The cross section of the cylinder is three-quarters of a circular path started at the lowermost point of the circle \(\displaystyle T\), and the tangent to the circle at point \(\displaystyle T\) is in the plane of the slope. A uniform solid disc of mass \(\displaystyle m\) and of radius \(\displaystyle r\) is released without any initial speed from the plane. (Static friction is big enough everywhere, so the disc rolls down the slope without sliding. Rolling friction is negligible. The cylindrical surface is ideally smooth.)
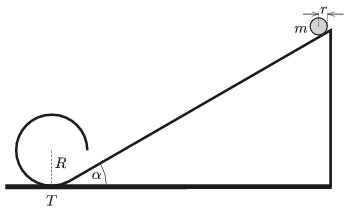
\(\displaystyle a)\) What is the radius of the disc if it just passes the gap below the cylinder?
\(\displaystyle b)\) What is the least height, measured from the ground, from which the disc should be released in order that it arrive back to the slope at a vertical velocity?
\(\displaystyle c)\) In this case what is the speed of the disc when it reaches the slope?
(5 pont)
Deadline expired on May 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Az 1. ábráról leolvasható, hogy ha a korong éppen átfér a hengerfelület alatt, akkor
\(\displaystyle R=R\sin\alpha+2r,\)
vagyis
\(\displaystyle r=R \frac{1-\sin\alpha}{2} =\frac{R}{4}=8~\rm cm.\)
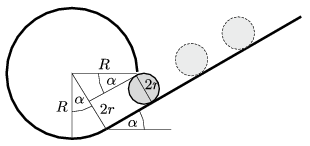
1. ábra
\(\displaystyle b)\) Legyen \(\displaystyle H\) a korong középpontjának magassága a vízszintes talajtól mérve az elengedés pillanatában. Itt a korong helyzeti energiája \(\displaystyle mgH\). A \(\displaystyle H\) magasságból induló korong a lejtőn gördül, a lejtő egyenes részének alján (ha ott a tömegközéppontjának sebessége \(\displaystyle v_0\))
\(\displaystyle E_1= \frac{1}{2}mv_0^2\)
transzlációs mozgási és
\(\displaystyle E_2= \frac{1}{2}\Theta \omega^2= \frac{1}{4}mv_0^2\)
forgási energiával rendelkezik. Az energiamegmaradás tétele szerint
\(\displaystyle mgH-mgR+mg(R-r)\cos\alpha =E_1+E_2.\)
A mozgás további részében a hengerfelület simasága miatt a forgási energia nem változik, ezért elegendő csak a transzlációs mozgás energiájával foglalkoznunk. A tömegközéppont \(\displaystyle R-r=0{,}24~\rm m\) sugarú körpályán mozog, és akkor nem válik el a körívtől annak legmagasabb pontjánál, ha az ottani \(\displaystyle v\) sebességére fennáll:
\(\displaystyle m\frac{v^2}{R-r}\ge mg.\)
A munkatétel szerint
\(\displaystyle m\frac{v^2}{2}=m\frac{v_0^2}{2}-mg(R-r)(1+\cos\alpha).\)
A fenti egyenletekből kapjuk, hogy
\(\displaystyle H\ge \frac{13}{4}R - \frac{9}{4}r + \frac{1}{2}(R-r)\,\cos\alpha=0{,}964~\rm m. \)
\(\displaystyle c)\) A hengerfelülettel érintkező korong tömegközéppontja a körpálya legmagasabb pontjánál
\(\displaystyle v=\sqrt{(R-r)g}\approx 1{,}53~\rm m/s\)
sebességgel mozog. Innen a körpálya végéig a tömegközéppont \(\displaystyle h_1\) távolságnyival kerül mélyebbre, majd függőleges hajítással mozogva a lejtőig további \(\displaystyle h_2\)-t süllyed. A munkatétel szerint a lejtőnek ütköző korong tömegközéppontjának sebessége
\(\displaystyle v_\text{ütk}=\sqrt{v^2+2g(h_1+h_2)}.\)
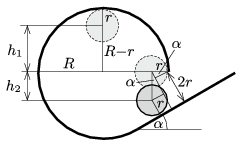
2. ábra
A 2. ábráról leolvasható, hogy
\(\displaystyle h_1=R-r=0{,}24~\rm m,\)
továbbá
\(\displaystyle 2r+r\sin\alpha=h_2\cos\alpha+r,\)
vagyis
\(\displaystyle h_2=\frac {1+\sin\alpha}{\cos\alpha}r\approx 0{,}14~\rm m,\)
és így a keresett sebesség: \(\displaystyle v_\text{ütk}\approx 3{,}13~\frac{\rm m}{\rm s}.\)
Statistics:
44 students sent a solution. 4 points: Makovsky Mihály. 3 points: 11 students. 2 points: 17 students. 1 point: 11 students. 0 point: 4 students.
Problems in Physics of KöMaL, April 2019
