 Problem P. 5134. (May 2019)
Problem P. 5134. (May 2019)
P. 5134. One end of a very thin negligible-mass rod of length \(\displaystyle R=0{.}64~\rm m\) is attached to a horizontal axle, whilst to its other end a small sphere of mass \(\displaystyle m=5\) g and of charge \(\displaystyle Q=6\cdot10^{-7}\) C is fixed. The whole structure is placed into vertically downward uniform electric field of strength \(\displaystyle E=2\cdot10^5\) V/m. The rod is put into the horizontal position shown in the figure.
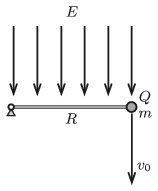
\(\displaystyle a)\) What vertically downward initial speed \(\displaystyle v_0\) should the small sphere be given in order that after 3/4 of a complete revolution the rod gets stuck, and at the same time the small sphere is ceased to be fixed to the rod, and flies back exactly to its initial position?
\(\displaystyle b)\) What is the angle between the velocity of the small sphere and the horizontal, when the sphere passes its initial position?
\(\displaystyle c)\) What is the ratio of the speed of the sphere when it passes its initial position to that of its initial value?
(5 pont)
Deadline expired on June 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A gömböcskére függőlegesen lefelé ható,
\(\displaystyle F=mg+QE=m\left(g+\frac{QE}{m}\right)\)
nagyságú erő hat. Ez az erő olyan, mintha csak a nehézségi erő hatna, de a gravitációs gyorsulás nem a szokásos nagyságú, hanem
\(\displaystyle g'=g+\frac{QE}{m}= \left( {9,81}+\frac{(6\cdot10^{-7})(2\cdot10^{5})}{ 5\cdot10^{-3} } \right)\frac{\rm m}{\rm s^2}=33{,}8~\frac{\rm m}{\rm s^2}\)
lenne.
\(\displaystyle a)\) Legyen a gömböcske sebessége a pályájának legmagasabb pontjánál \(\displaystyle v_1\). Ha visszajut a kiindulási helyére, a vízszintes hajítás összefüggései szerint fennáll, hogy
\(\displaystyle v_1t=R, \qquad \frac{g'}{2}t^2=R,\)
ezekből
\(\displaystyle v_1=\sqrt{\frac{g'R}{2}}\)
következik. Másrészt a munkatétel szerint
\(\displaystyle \frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2=-mg'R,\)
vagyis
\(\displaystyle v_0=\sqrt{v_1^2+2g'R}=\sqrt{\frac52g'R}=7{,}36~\frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) A kiindulási helyére visszaérkező test vízszintes sebessége \(\displaystyle v_1\), függőleges sebessége pedig \(\displaystyle R\) magasságból történő szabadesés sebessége, vagyis
\(\displaystyle v_2=\sqrt{2g'R}.\)
A test sebességvektora tehát
\(\displaystyle \arctg\frac{v_2}{v_1}=\arctg 2=63{,}4^\circ \)
nagyságú szöget zár be a vízszintessel.
\(\displaystyle c)\) A kiindulási helyre való visszaérkezéskor a sebesség nagysága:
\(\displaystyle v_3=\sqrt{v_1^2+v_2^2}=\sqrt{\frac52g'R}=7{,}36~\frac{\rm m}{\rm s},\)
ami éppen \(\displaystyle v_0\)-lal egyezik meg. Ez az eredmény a munkatételből közvetlenül is leolvasható. A kérdezett arány tehát 1.
Statistics:
40 students sent a solution. 5 points: Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Bukor Benedek, Endrész Balázs, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Jánosik Áron, Keltai Dóra, Kertész Balázs, Ludányi Levente, Mácsai Dániel, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Sal Dávid, Sümegi Géza, Tiefenbeck Flórián, Toronyi András, Varga Vázsony, Vass Bence, Vaszary Tamás, Viczián Anna, Zámbori Zalán. 4 points: Elek Péter, Györgyfalvai Fanni, Lipták Gergő, Németh Csaba Tibor, Schneider Anna. 3 points: 4 students. 2 points: 2 students.
Problems in Physics of KöMaL, May 2019
