 Problem P. 5136. (May 2019)
Problem P. 5136. (May 2019)
P. 5136. Both ends of a thread are attached to the top two vertices of a rectangular picture of sides \(\displaystyle A\) and \(\displaystyle B\), and then the picture is hung to a peg. What should the least length of the thread be in order that the picture remain in a stable symmetric position? Friction between the peg and the thread is negligible, and the centre of mass of the picture coincides with the geometric centre of the rectangle.
(5 pont)
Deadline expired on June 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a fonál hosszát \(\displaystyle L\)-lel, és legyen a fonál két vége a kép egyik, \(\displaystyle A\) hosszúságú oldalának \(\displaystyle F_1\) és \(\displaystyle F_2\) végpontjához rögzítve.
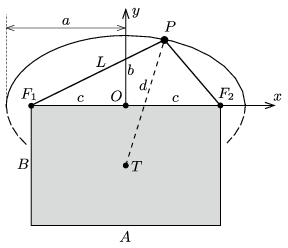
Adjuk meg a képtartó szög (az ábrán a \(\displaystyle P\) pont) helyét az \(\displaystyle F_1\) és \(\displaystyle F_2\) pontok \(\displaystyle O\) felezőpontján átmenő, a téglalap oldalaival párhuzamos tengelyű \(\displaystyle (x,y)\) derékszögű koordináta-rendszerben! A fonál hosszának állandóságából következik, hogy a \(\displaystyle P\) pont rajta fekszik az \(\displaystyle F_1\) és \(\displaystyle F_2\) fókuszpontú,
\(\displaystyle a=\frac{L}{2}, \qquad b=\frac{\sqrt{L^2-A^2}}{2} \)
féltengelyű ellipszisen. Az ellipszis egyenlete:
\(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\)
vagyis
\(\displaystyle y=b\sqrt{1-\frac{x^2}{a^2}},\)
ami a kép méreteivel és a fonál hosszával kifejezve így írható:
\(\displaystyle y=\frac{\sqrt{L^2-A^2}}{2}\sqrt{1-\frac{4x^2}{L^2}}.\)
A szögre akasztott kép egyensúlyi helyzetben úgy helyezkedik el, hogy a \(\displaystyle P\)-re és \(\displaystyle T\)-re illeszkedő egyenes függőleges legyen. A kép helyzeti energiája a \(\displaystyle d=PT\) hossznak \(\displaystyle (-1)\)-szeresével arányos. Ha a szimmetrikus helyzetben (vagyis \(\displaystyle (x=0\)-nál) a \(\displaystyle d(x)\) függvénynek (és ezzel együtt \(\displaystyle d^2(x)\)-nek is) lokális maximuma van, akkor ez a helyzet stabil, ha viszont minimuma van, akkor az egyensúly labilis, a kép a legkisebb külső zavar hatására valamelyik oldalra kibillen.
Vizsgáljuk meg \(\displaystyle \left[d(x)\right]^2\) viselkedését a szimmetrikus helyzethez közeli (vagyis \(\displaystyle x\ll A\)-val jellemzett) tartományban:
\(\displaystyle \left[d(x)\right]^2=x^2+\left(y+\frac{B}{2}\right)^2=x^2+\left(b\sqrt{1-\frac{x^2}{a^2}}+\frac{B}{2}\right)^2.\)
Alkalmazva az \(\displaystyle \varepsilon\ll 1\) esetén érvényes
\(\displaystyle \sqrt{1+\varepsilon}\approx 1+\frac{\varepsilon}{2}\)
összefüggést, a vizsgált kifejezés közelítőleg így írható:
\(\displaystyle \left[d(x)\right]^2\approx x^2+\left(b -b\frac{x^2}{2a^2}+\frac{B}{2}\right)^2\approx \left(b+\frac{B}{2}\right)^2+ x^2 \left[1- \left(b+\frac{B}{2}\right)\frac{b}{a^2} \right].\)
A stabilitást a szögletes zárójelben álló kifejezés előjele dönti el. A kép helyzete stabil, ha
\(\displaystyle 1- \left(\frac{\sqrt{L^2-A^2}}{2} +\frac{B}{2}\right)\frac{2\sqrt{L^2-A^2}}{L^2} <0,\)
vagyis
\(\displaystyle 1<\frac{L^2-A^2}{L^2}+B\frac{\sqrt{L^2-A^2}}{L^2},\)
\(\displaystyle A^2<B\sqrt{L^2-A^2},\)
tehát
\(\displaystyle L>\frac{A}{B}\sqrt{A^2+B^2}.\)
Hasonlóan egyszerű a számolás, ha \(\displaystyle d^2\)-et \(\displaystyle y\)-nal fejezzük ki:
\(\displaystyle \left[d(y)\right]^2=a^2-a^2\frac{y^2}{b^2}+\left(y+\frac{B}{2}\right)^2,\)
de a \(\displaystyle 0<y<b\) feltételnek is teljesülnie kell. Ennek a másodfokú függvénynek \(\displaystyle y^*=\frac{b^2B}{2(a^2-b^2)}\)-nél van maximuma (parabolacsúcs). Ha ez az az érték \(\displaystyle b\)-nél kisebb, akkor ott van \(\displaystyle d^2\) maximuma, és a kép ferdén áll. Ha \(\displaystyle y^*\ge b\), akkor a tényleges maximum \(\displaystyle y=b\)-nél van, és a kép egyenesen áll. A
\(\displaystyle \frac{b^2B}{2(a^2-b^2)}\ge b\)
feltétel \(\displaystyle A\)-val és \(\displaystyle B\)-vel kifejezve:
\(\displaystyle L>\frac{A}{B}\sqrt{A^2+B^2}.\)
Statistics:
9 students sent a solution. 5 points: Elek Péter, Markó Gábor, Marozsák Tádé, Olosz Adél, Tiefenbeck Flórián. 4 points: Lipták Gergő. 2 points: 2 students. 0 point: 1 student.
Problems in Physics of KöMaL, May 2019
