 Problem P. 5141. (May 2019)
Problem P. 5141. (May 2019)
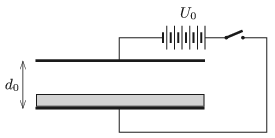
P. 5141. The plates of a parallel-plate condenser shown in the figure are horizontal and they are at a distance of \(\displaystyle d_0=4\) cm from each other. The condenser is in vacuum. An aluminium sheet of width \(\displaystyle d_0/4\) is placed on the lower plate, and high voltage is connected to the condenser.
\(\displaystyle a)\) What should the value of \(\displaystyle U_0\) be in order that the sheet rise?
\(\displaystyle b)\) At a given applied voltage of \(\displaystyle U\) what is the width of the aluminium sheet that can rise from the lower plate of the condenser of plate distance \(\displaystyle d_0\)?
\(\displaystyle c)\) Is there a voltage value at which the sheet surely rises, independently of the width of the sheet (provided that it is less than \(\displaystyle d_0\))?
(Assume that the aluminium sheet remains horizontal all the time. The sides of the condenser plates are much greater than \(\displaystyle d_0\), and wind effects are negligible.)
(5 pont)
Deadline expired on June 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Az alumíniumlemez behelyezésekor a megosztás miatt olyan síkkondenzátor alakul ki, amelynél a lemeztávolság \(\displaystyle d=\tfrac34 d_0\). Ismeretes, hogy a síkkondenzátor két lemeze közötti vonzóerő az
\(\displaystyle F=\frac{\varepsilon_0 U_0^2 A}{2d^2}\)
összefüggéssel számítható ki, ahol \(\displaystyle A\) a fegyverzetek alapterülete. A \(\displaystyle \varrho=2700~\rm kg/m^3\) sűrűségű alumíniumlemez súlya:
\(\displaystyle G=\frac{d_0}{4}A\varrho g.\)
A lemez akkor emelkedik fel, ha \(\displaystyle F>G\), vagyis
\(\displaystyle U_0>\frac{3}{4}d_0\sqrt{\frac{\varrho g d_0}{2\varepsilon_0}}\approx 232~\rm kV.\)
\(\displaystyle b)\) Helyezzünk bele most egy \(\displaystyle xd_0\) vastagságú alumíniumlemezt a kondenzátorba (\(\displaystyle 0<x<1\)). A lemez megemelkedésének feltétele:
\(\displaystyle \frac{\varepsilon_0 U^2}{2\varrho g d_0^3}> x(1-x)^2\equiv f(x).\)
Az ábra \(\displaystyle f(x)\) grafikonját és a megemelkedés feltételét mutatja. Adott (de nem túl nagy) \(\displaystyle U\) esetén ez a feltétel akkor teljesül, ha \(\displaystyle x<x_1\) vagy \(\displaystyle x>x_2\), azaz az alumíniumlemez elég vékony (könnyű), vagy elég vastag, emiatt viszonylag közel kerül a felső kondenzátorlemezhez.
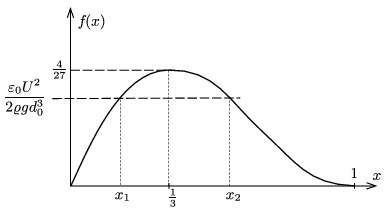
\(\displaystyle c)\) Az \(\displaystyle f(x)\) függvénynek \(\displaystyle x=\tfrac13\)-nál maximuma van, és a maximum értéke \(\displaystyle \tfrac 4{27}\). Ezt differenciálszámítással, vagy a számtani-mértani középre vonatkozó egyenlőtlenség segítségével láthatjuk be:
\(\displaystyle \sqrt[3]{2f(x)}=\sqrt[3]{(2x)(1-x)(1-x)}\le \frac{(2x)+(1-x)+(1-x)}{3}=\frac{2}{3},\)
azaz
\(\displaystyle f(x)\le \frac{4}{27}.\)
(Az egyenlőség \(\displaystyle 2x=1-x\), azaz \(\displaystyle x=\tfrac13\)-nál teljesül, itt lesz \(\displaystyle f(x)\) maximuma.)
Amennyiben
\(\displaystyle U>U_ \text{krit}=\frac{2}{3}d_0\sqrt{\frac{2\varrho g d_0}{3\varepsilon_0}}= 238~\rm kV,\)
az adott lemeztávolságú kondenzátorban semmilyen vastag alumíniumlemez nem maradhat nyugalomban az alsó fegyverzeten.
Statistics:
18 students sent a solution. 5 points: Bokor Endre, Bonifert Balázs, Elek Péter, Mácsai Dániel, Makovsky Mihály, Marozsák Tádé, Sal Dávid, Tiefenbeck Flórián, Viczián Anna. 4 points: Vaszary Tamás. 2 points: 4 students. 1 point: 4 students.
Problems in Physics of KöMaL, May 2019
