 Problem P. 5147. (September 2019)
Problem P. 5147. (September 2019)
P. 5147. An air-plane day is organised at Pécs-Pogány airport. For advertisement purposes a helium-filled balloon of volume \(\displaystyle V=10~\rm m^3\) is launched. The balloon is tethered by a piece of rope of negligible mass. The volume of the fabric of the envelope is negligible, its mass, without the inside gas, is \(\displaystyle m=2~\rm kg\). The temperature inside the envelope, and outside, next to the balloon is \(\displaystyle T=300~\)K, whilst the ambient air pressure is \(\displaystyle p_0=10^5\) Pa. The pressure due to the elasticity of the fabric of the envelope can be neglected.
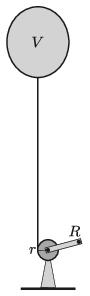
At the end of the event the balloon is slowly winched down. The radius of the drum of the winch is \(\displaystyle r=10\) cm, whilst the radius of the crank is \(\displaystyle R=30\) cm. Air drag is negligible.
\(\displaystyle a)\) What is the magnitude of the force applied on the crank, if the balloon is pulled down uniformly?
\(\displaystyle b)\) What is the power output when the balloon is winched down, if the balloon descends at a speed of \(\displaystyle v=1\) m/s?
(4 pont)
Deadline expired on October 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A hélium moláris tömege \(\displaystyle M_\text{He}=4\) g/mol, a levegő átlagos moláris tömege \(\displaystyle M_\text{lev.}=29\) g/mol. A gáztörvényből kiszámíthatjuk a hélium és a kiszorított levegő tömegét:
\(\displaystyle m_\text{He}=\frac{p_0 V}{RT}M_\text{He}=1{,}6~\rm kg,\)
\(\displaystyle m_\text{lev.}=\frac{p_0 V}{RT}M_\text{lev.}=11{,}6~\rm kg.\)
Az egyenletesen mozgó ballonra ható erők eredője nulla:
\(\displaystyle F+ m_\text{He}g+mg-m_\text{lev.}g=0,\)
ahonnan a kötelet feszítő erő:
\(\displaystyle F=\left(m_\text{lev.}-m_\text{He}-m\right)g=8{,}0~{\rm kg}\cdot 9{,}81~\frac{\rm m}{\rm s^2}=78{,}5~\rm N.\)
\(\displaystyle a)\) A hajtókarra (a csörlőre ható forgatónyomatékok egyensúlya miatt) \(\displaystyle F'=\frac{r}{R}F=\frac{1}{3}F=26{,}2~\rm N\) erőt kell kifejteni.
\(\displaystyle b)\) A ballon lehúzásához szükséges teljesítmény: \(\displaystyle P=Fv=78{,}5~\rm W.\)
Statistics:
71 students sent a solution. 4 points: Amrein Roland, Bánáti Tamás, Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Dékány Csaba, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Gurzó József, Györgyfalvai Fanni, Hartmann Alice, Jánosik Áron, Kardkovács Levente, Kis-Bogdán Kolos, Laposa Hédi, Lengyel Barnabás, Ludányi Levente, Mihalik Bálint, Németh Kristóf, Perényi Barnabás, Schneider Anna, Selmi Bálint, Somlán Gellért, Szabó 314 László, Szikora 417 Viktor, Tanács Kristóf, Tanner Norman, Toronyi András, Török 111 László, Vass Bence. 3 points: 24 students. 2 points: 9 students. 1 point: 4 students. 0 point: 1 student.
Problems in Physics of KöMaL, September 2019
