 Problem P. 5156. (October 2019)
Problem P. 5156. (October 2019)
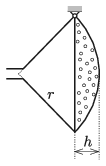
P. 5156. The spherical sector shaped rose of a watering can, made of thin metal, is hung at one point on its circular rim by means of a hinge (see the figure). What is the ratio \(\displaystyle h/r\), if in the equilibrium position of the rose its symmetry axis is horizontal? (The metal sheet has constant width and uniform density. The size of the tube through which the water enters the rose, as well as the total area of the small holes can be considered negligibly small.)
(5 pont)
Deadline expired on November 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a vékony lemez egységnyi felületű darabjának tömegét (felületi tömegsűrűségét) \(\displaystyle \eta\)-val, a peremkörének sugarát pedig \(\displaystyle R\)-rel. Ez utóbbi kifejezhető \(\displaystyle r\)-rel és \(\displaystyle h\)-val:
\(\displaystyle R^2+(r-h)^2=r^2,\qquad \text{vagyis}\qquad R=\sqrt{h(2r-h)}.\)
A locsolókanna-rózsa gömbszelet alakú részének tömege
\(\displaystyle m_1=\eta 2r\pi h,\)
és ennek a résznek a tömegközéppontja
\(\displaystyle x_1=\frac{h}{2}\)
távol esik a csuklón átmenő és a szimmetriatengelyre merőleges síktól.
A locsolókanna-rózsa kúppalást alakú részének tömege
\(\displaystyle m_2=\eta r\pi \sqrt{h(2r-h)},\)
és a tömegközéppont távolsága az előbb említett síktól
\(\displaystyle x_2=\frac{r-h}{3}.\)
Megjegyzés. A tömegközéppont helyét pl. úgy is megkaphatjuk, hogy összehasonlítjuk a képzeletben egyenletes vastagságú részekre szeletelt kúppalást egyes darabjaira ható nehézségi erőt egy – ugyancsak egyenközűen felszeletelt – derékstögű háromszög alakú lemez részeire ható erővel. Mindkét esetben a nehézségi erő nagysága a szeletek sorszámával arányosan, lineárisan változik, tehát mindkét alakzat tömegközéppontja ugyanott, a magasság egyharmadánál lesz.
A kanna rózsája akkor maradhat egyensúlyban vízszintes szimmetriatengellyel, ha a csuklóra vonatkoztatva a két rész súlyának forgatónyomatéka megegyezik:
\(\displaystyle m_1gx_1=m_2gx_2,\)
azaz
\(\displaystyle 2\pi r h \cdot \frac{h}{2}\cdot \eta g= r\pi \sqrt{h(2r-h)}\cdot \frac{r-h}{3}\cdot \eta g.\)
Ebből a \(\displaystyle \lambda=h/r\) dimenziótlan arányszámra (algebrai átalakítások után) a
\(\displaystyle 10\lambda^3-4\lambda^2+5\lambda-2\equiv (5\lambda-2)(2\lambda^2+1)=0\)
harmadfokú egyenletet kapjuk. Látható, hogy ennek egyetlen valós gyöke:
\(\displaystyle \lambda=\frac{2}{5}=0{,}4.\)
Statistics:
25 students sent a solution. 5 points: Bohács Tamás, Bokor Endre, Bonifert Balázs, Fülöp Sámuel Sihombing, Pálfi Fanni, Pankotai Dóra Anna, Somlán Gellért, Vass Bence. 4 points: Varga Vázsony. 3 points: 2 students. 2 points: 4 students. 1 point: 3 students. 0 point: 7 students.
Problems in Physics of KöMaL, October 2019
