 Problem P. 5169. (November 2019)
Problem P. 5169. (November 2019)
P. 5169. One end of a uniform-density rod of mass \(\displaystyle m=0.4\) kg and of length \(\displaystyle L=20\) cm is attached to a hinge at point \(\displaystyle A\), as shown in the left figure, about which it can be rotated in any direction. The other end of the rod is attached to a vertical spring of spring constant \(\displaystyle D=25\) N/m, which also has a length of \(\displaystyle L\) when there is no force exerted on it. Initially the spring and the rod are in the same line. Then the rod is displaced (as it is shown in the right figure) by an angle of \(\displaystyle \varphi=60^\circ\), and then it is released.
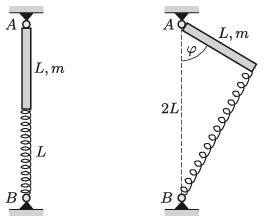
\(\displaystyle a)\) What is the speed of the end of the rod when it passes the vertical position?
\(\displaystyle b)\) The rod is displaced from the equilibrium position by a small angle, and then it is released. How long does it take for the rod to reach the vertical position?
\(\displaystyle c)\) By what angular speed should the spring-rod system be rotated about the vertical axis \(\displaystyle AB\) in order that the angle between the rod and the vertical be constantly \(\displaystyle 60^\circ\)?
(Friction is negligible everywhere.)
(5 pont)
Deadline expired on December 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) A kitérített rúd, a megfeszített rugó és az \(\displaystyle AB\) szakasz derékszögű háromszöget alkot, a rugó hossza tehát \(\displaystyle \sqrt{3}\,L\), a megnyúlása pedig \(\displaystyle (\sqrt{3}-1)L\) lesz. A rúd tehetetlenségi nyomatéka az \(\displaystyle A\) pontra vonatkoztatva \(\displaystyle \tfrac13mL^2\), és a tömegközéppontja a függőleges helyzet eléréséig \(\displaystyle L/4\) távolsággal kerül mélyebbre. Alkalmazva a mechanikai energiamegmaradás tételét:
\(\displaystyle \frac{1}{2}D(\sqrt{3}-1)^2L^2+\frac{1}{4}mgL=\frac12\cdot \frac13 mL^2\omega^2,\)
ahonnan az adatok behelyettesítése után a rúd szögsebességére az \(\displaystyle \omega=13{,}2\, {\rm s}^{-1},\) a rúd végpontjának sebességére pedig a \(\displaystyle v=L\omega=2{,}64~\frac{\rm m}{\rm s}\) eredmény adódik.
\(\displaystyle b)\) A rudat kis szöggel kitérítve a rugó megnyúlása (és ezzel arányosan a rugóban ébredő erő) a kitérés négyzetével arányos, a rugóerőnek az \(\displaystyle A\) pontra vonatkozó forgatónyomatéka pedig közelítőleg a kitérés köbével arányos. Ez a forgatónyomaték a nehézségi erőnek a kitéréssel arányos forgatónyomatéka mellett elhanyagolhatóan kicsi, a rendszer tehát úgy mozog, mintha a rugó nem is volna ott. Ez annyit jelent, hogy a rúd mozgása olyan fizikai ingaként tárgyalható, amelynek lengésideje:
\(\displaystyle T=2\pi\frac{\frac13 mL^2}{\frac14 mgL}=\sqrt{\frac{2L}{3g}}=0{,}73~\rm s.\)
A kitérített, majd kezdősebesség nélkül elengedett rúd
\(\displaystyle \frac {T}4=0{,}18~\rm s\)
alatt kerül függőleges helyzetbe.
\(\displaystyle c)\) A rúd valamekkora \(\displaystyle \omega\) szögsebességgel forgó rendszerből nézve egyensúlyi helyzetben van, ezért az erők forgatónyomatékának előjeles összege nulla. A rúdra – ebben a forgó, nem inerciarendszerben – négyféle erő hat:
1. A \(\displaystyle G=mg=3{,}92~\)N nagyságú nehézségi erő, amelynek hatásvonala az \(\displaystyle A\) ponttól \(\displaystyle \tfrac12 L\,\sin 60^\circ=0{,}34~\rm m\) távol van.
2. A megfeszített rugóban fellépő erő nagysága \(\displaystyle F_1=D(\sqrt{3}-1)L=3{,}66~\rm N\), és a hatásvonala \(\displaystyle L=0{,}2~\rm m\) távol van az \(\displaystyle A\) ponttól.
3. A ,,centrifugális erő'', amelynek nagysága a tömegközéppontba képzelt \(\displaystyle m\) tömegű testre ható tehetetlenségi erő nagyságával egyezik meg: \(\displaystyle F_2=\tfrac12 mL\sin 60^\circ\,\omega^2=\omega^2\cdot 0{,}0346~\rm N\,s^2.\) Ennek az erőnek a hatásvonala azonban nem a tömegközépponton, hanem a rúd alsó harmadolópontján halad keresztül, tehát az \(\displaystyle A\) ponttól mért távolsága \(\displaystyle \tfrac23L\cos 60^\circ=0{,}0667~\rm m.\)
4. A rúdra hat még az \(\displaystyle A\) pontban (a csuklónál) egy ismeretlen nagyságú és ismeretlen irányú kényszererő, ennek azonban nincs forgatónyomatéka az \(\displaystyle A\) ponton átmenő tengelyre vonatkozóan.
Az erők forgatónyomatékának egyensúlyi feltétele:
\(\displaystyle F_1 L+G\frac{L}{2}\sin 60^\circ=\tfrac23L\cos 60^\circ F_2,\)
vagyis
\(\displaystyle 3{,}66\cdot 0{,}20+3{,}92\cdot 0{,}087= 0{,}0346~\rm s^2\cdot 0{,}0667 \cdot \omega^2.\)
Ebből a szögsebesség kiszámítható:
\(\displaystyle \omega=21{,}5~\frac{1}{\rm s}.\)
Statistics:
27 students sent a solution. 5 points: Vass Bence. 4 points: Fiam Regina, Fonyi Máté Sándor, Ludányi Levente, Szász Levente, Varga Vázsony. 3 points: 7 students. 2 points: 6 students. 1 point: 7 students. 0 point: 1 student.
Problems in Physics of KöMaL, November 2019
