 Problem P. 5184. (December 2019)
Problem P. 5184. (December 2019)
P. 5184. A high-resolution diffraction grating can deflect a laser beam which enters perpendicularly to the grating, such that the angle of the first order maximum is \(\displaystyle 45^\circ\). What happens if another similar diffraction grating is placed into the path of the diffracted beam such that it is
\(\displaystyle a)\) parallel to the original diffraction grating;
\(\displaystyle b)\) perpendicular to the original diffraction grating?
(The slits of the gratings are parallel to each other in both cases.)
(5 pont)
Deadline expired on January 10, 2020.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A \(\displaystyle d\) rácsállandójú optikai rácson \(\displaystyle \lambda\) hullámhosszúságú fény olyan \(\displaystyle \alpha_n\) szögben hajlik el, amelyre
\(\displaystyle \sin\alpha_n=n\,\frac{\lambda}{d}; \qquad n=0, \pm 1; \pm 2\ldots.\)
Esetünkben \(\displaystyle \alpha_1=45^\circ,\) ahonnan \(\displaystyle \lambda=d/\sqrt 2\) következik. Egy ilyen rácsnál az elhajlás rendje csak \(\displaystyle n=-1, 0, +1\) lehet, \(\displaystyle \vert n \vert \ge 2\) esetén az
\(\displaystyle \sin\alpha_n=\frac{n}{ \sqrt{2}}\)
egyenletnek nincs (valós) megoldása.
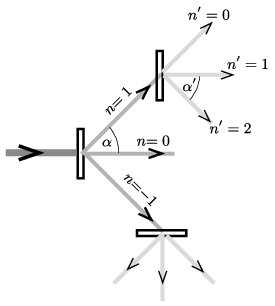
\(\displaystyle a)\) Az elhajló sugarak útjába \(\displaystyle 45^\circ\)-os szögben helyezett, az elsővel megegyező tulajdonságú és azzal párhuzamos rács szomszédos réseire \(\displaystyle \pm d\sin 45^\circ=d/\sqrt{2}\) útkülönbséggel érkeznek a fényhullámok, így most a felület normálisától mért \(\displaystyle \alpha'\) szöggel kifejezve az erősítés feltételét ezt kapjuk:
\(\displaystyle \frac{d}{\sqrt2}+d\sin\alpha'=n'\,\lambda=n'\frac{d}{\sqrt2},\qquad \text{vagyis}\qquad \sin\alpha'=\frac{n'-1}{\sqrt2}.\)
Most csak az \(\displaystyle n'=2,\,1~\text{és}~0\) számokkal jelzett rendek valósulnak meg, és a megfelelő szögek:
\(\displaystyle \alpha_2'= 45^\circ,\qquad \alpha_1'=0,\qquad \alpha_2'= -45^\circ.\)
\(\displaystyle b)\) Ugyanez a helyzet a merőlegesen álló rácsoknál is, az elhajlás szöge itt is (a rács normálisától mérve) csak \(\displaystyle \pm 45^\circ\) vagy nulla lehet.
A kétféleképpen álló rácson elhajló sugarakat az ábra mutatja. A rácsok nemcsak ,,előrefelé'', hanem visszafelé is szórják a fényt, ugyanolyan szögben, mint előre. Ezeket a fénysugarakat az ábrán az áttekinthetőség kedvéért nem tüntettük fel.
Statistics:
7 students sent a solution. 5 points: Fülöp Sámuel Sihombing, Selmi Bálint. 3 points: 2 students. 1 point: 2 students. 0 point: 1 student.
Problems in Physics of KöMaL, December 2019
